| HEAD | PREVIOUS |
Chapter 1
Fitting Functions to Data
1.1 Exact fitting
1.1.1 Introduction
Suppose we have a set of real-number data pairs . These can be considered to be a set of points in the -plane. They can also be thought of as a set of values of a function of ; see Fig. 1.1.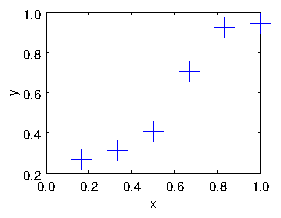 A frequent challenge is to find some kind of function that
represents a "best fit" to the data in some sense. If the data were
fitted perfectly, then clearly the function would have the property
A frequent challenge is to find some kind of function that
represents a "best fit" to the data in some sense. If the data were
fitted perfectly, then clearly the function would have the property
1.1.2 Representing an exact fitting function linearly
We have an infinite choice of possible fitting functions. Those functions must have a number of different adjustable parameters that are set so as to adjust the function to fit the data. One example is a polynomial.1.1.3 Solving for the coefficients
When we have a matrix equation of the form , where is a square matrix, then provided that the matrix is non-singular, that is, provided its determinant is non-zero, , it possesses an inverse . Multiplying on the left by this inverse we get: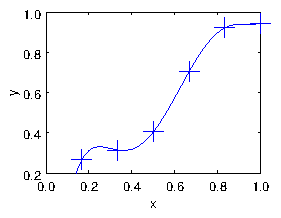 polynomial (with 6 terms including the 1) to the six points of our
data. The line goes exactly through every point. But there's a
significant problem that the line is unconvincingly curvy near its
ends. It's not a terribly good fit.
polynomial (with 6 terms including the 1) to the six points of our
data. The line goes exactly through every point. But there's a
significant problem that the line is unconvincingly curvy near its
ends. It's not a terribly good fit.
1.2 Approximate Fitting
If we have lots of data which has scatter in it, arising from uncertainties or noise, then we almost certainly do not want to fit a curve so that it goes exactly through every point. For example see Fig. 1.3.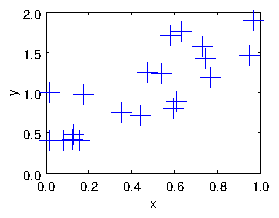 What do we do then? Well, it turns out that we can use almost exactly
the same approach, except with different number of points ()
and terms () in our linear fit. In other
words we use a representation
What do we do then? Well, it turns out that we can use almost exactly
the same approach, except with different number of points ()
and terms () in our linear fit. In other
words we use a representation
1.2.1 Linear Least Squares
What do we mean by "best fit"? Especially when fitting a function of the linear form eq. (1.7), we usually mean that we want to minimize the vertical distance between the points and the line. If we had a fitted function , then for each data pair , the square of the vertical distance between the line and the point is . So the sum, over all the points, of the square distance from the line is1.2.2 SVD and the Moore-Penrose Pseudo-inverse
We seem to have gone off in a different direction from our original way to solve for the fitting coefficients by inverting the square matrix . How is that related to the finding of the least-squares solution to the over-specified set of equations (1.8)? The answer is a piece of matrix magic! It turns out that there is (contrary to what one is taught in an elementary matrix course) a way to define the inverse of a non-square matrix or of a singular square matrix. It is called the (Moore-Penrose) pseudo-inverse. And once found it can be used in essentially exactly the way we did for the non-singular square matrix in the earlier treatment. That is, we solve for the coefficients using , except that is now the pseudo-inverse. The pseudo-inverse is best understood from a consideration of what is called the Singular Value Decomposition (SVD) of a matrix. This is the embodiment of a theorem in matrix mathematics that states that any matrix can always be expressed as the product of three other matrices with very special properties. For our matrix this expression is:- is an orthonormal matrix
- is an orthonormal matrix
- is an diagonal matrix
1.2.3 Smoothing and Regularization
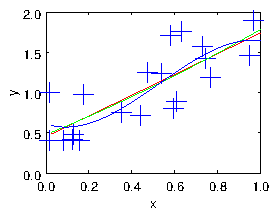
As we illustrate in Fig. 1.4, by choosing the number of degrees of freedom of the fitting function one can adjust the smoothness of the fit to the data. However, the choice of basis functions then constrains one in a way that has been pre-specified. It might not in fact be the best way to smooth the data to fit it by (say) a straight line or a parabola. A better way to smooth is by "regularization" in which we add some measure of roughness to the residual we are seeking to minimize. The roughness (which is the inverse of the smoothness) is a measure of how wiggly the fit line is. It can in principle be pretty much anything that can be written in the form of a matrix times the fit coefficients. I'll give an example in a moment. Let's assume the roughness measure is homogeneous, in the sense that we are trying to make it as near zero as possible. Such a target would be , where is a matrix of dimension , where is the number of distinct roughness constraints. Presumably we can't satisfy this equation perfectly because a fully smooth function would have no variation, and be unable to fit the data. But we want to minimize the square of the roughness . We can try to fulfil the requirement to fit the data, and to minimize the roughness, in a least-squares sense by constructing an expanded compound matrix system combining the original equations and the regularization, thus1.3 Tomographic Image Reconstruction
Consider the problem of x-ray tomography. We make many measurements of the integrated density of matter along chords in a plane section through some object whose interior we wish to reconstruct. These are generally done by measuring the attenuation of x-rays along each chord, but the mathematical technique is independent of the physics. We seek a representation of the density of the object in the form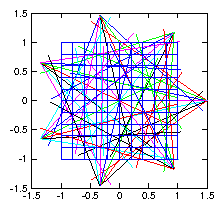
Figure 1.5: Illustrative layout of
tomographic reconstruction of density in a plane
using multiple fans of chordal observations.
Each chord along which measurements are made, passes through the basis
functions (e.g. the pixels), and for a particular set of coefficients
we therefore get a chordal measurement value
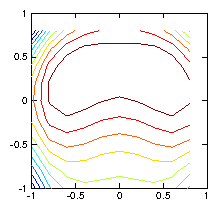
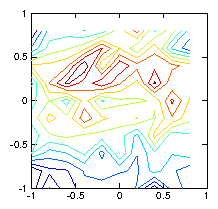
Figure 1.6: Contour plots of the initial test -function (left) used to
calculate the chordal integrals, and its reconstruction based upon
inversion of the chordal data (right). The number of pixels (100)
exceeds the number of views (49), and the number of singular
values used in the pseudo inverse is restricted to 30. Still they
do not agree well, because various artifacts appear. Reducing the
number of singular values does not help.
We then almost certainly want to smooth the representation
otherwise all sorts of meaningless artifacts will
appear in our reconstruction that have no physical existence. If we
try to do this by forming a pseudo-inverse in which a smaller number
of singular values are retained, and the others put to zero, there is
no guarantee that this will get rid of the roughness. Fig. 1.6 gives an example.
If we instead smooth the reconstruction by regularization, using as
our measure of roughness the discrete (2-D) Laplacian
() evaluated at each pixel. We get a far better result,
as shown in Fig. 1.7. It turns out that this good result
is rather insensitive to the value of over two or three
orders of magnitude.
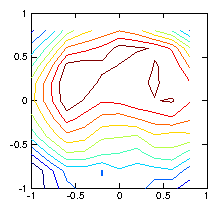
Figure 1.7: Reconstruction using a regularization smoothing based upon
. The contours are much nearer to reality.
1.4 Efficiency and Nonlinearity
Using the inverse or pseudo-inverse to solve for the coefficients of a fitting function is intuitive and straight-forward. However, in many cases it is not the most computationally efficient approach. For moderate size problems, modern computers have more than enough power to overcome the inefficiencies, but in a situation with multiple dimensions, such as tomography, it is easy for the matrix that needs to be inverted to become enormous, because that matrix's side length is the total number of pixels or elements in the fit, which may be, for example, the product of the side lengths nxny. The giant matrix that has to be inverted, may be very "sparse", meaning that all but a very few of its elements are zero. It can then become overwhelming in terms of storage and cpu to use the direct inversion methods we have discussed here. We'll see other approaches later. Some fitting problems are nonlinear. For example, suppose one had a photon spectrum of a particular spectral line to which one wished to fit a Gaussian function of particular center, width, and height. That's a problem that cannot be expressed as a linear sum of functions. In that case fitting becomes more elaborate, and less reliable. There are some potted fitting programs out there, but it's usually better if you can avoid them.Worked Example: Fitting sinusoidal functions
Suppose we wish to fit a set of data spread over the range of independent variable . And suppose we know the function is zero at the boundaries of the range, at and . It makes sense to incorporate our knowledge of the boundary values into the choice of functions to fit, and choose those functions to be zero at and . There are numerous well known sets of functions that have the property of being zero at two separated points. The points where standard functions are zero are of course not some arbitrary and . But we can scale the independent variable so that and are mapped to the appropriate points for any choice of function set. Suppose the functions that we decide to use for fitting are sinusoids: all of which are zero at and . We can make this set fit our range by using the scaling% Suppose x and y exist as column vectors of length N. (Nx1 matrices) j=[1:M]; % Create a 1xM matrix containing numbers 1 to M. theta=pi*(x-a)/(b-a); % Scale x to obtain the column vector theta. S=sin(theta*j); % Construct the matrix S using an outer product. Sinv=pinv(S); % Pseudo invert it. c=Sinv*y; % Matrix multiply y to find the coefficients c.The fit can then be evaluated for any value (or array) xfit, in the form effectively of a scalar product of with . The code is likewise astonishingly brief, and will need careful thought (especially noting what the dimensions of the matrices are) to understand what is actually happening.
yfit=sin(pi*(xfit-a)/(b-a)*j)*c; % Evaluate the yfit at any xfitAn example is shown in Fig. 1.8.
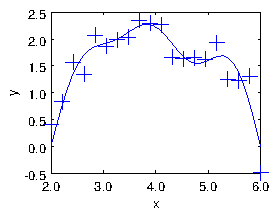
Figure 1.8: The result of the fit of sinusoids up to to a noisy
dataset of size . The points are the input data. The curve is
constructed by using the yfit expression on an
xfit array of some convenient length spanning the -range, and
then simply plotting yfit versus
xfit.
Exercise 1. Data fitting
1. Given a set of values of a function at the positions , write a short code to fit a polynomial having order one less than (so there are coefficients of the polynomial) to the data. Obtain a set of 6 numbers from http://silas.psfc.mit.edu/22.15/15numbers.html (or if that is not accessible use ). Take the values to be at the positions . Run your code on this data and find the coefficients . Plot together (on the same plot) the resulting fitted polynomial representing (with sufficient resolution to give a smooth curve) and the original data points, over the domain . Submit the following as your solution:- Your code in a computer format that is capable of being executed.
- The numeric values of your coefficients .
- Your plot.
- Brief commentary ( words) on what problems you faced and how you solved them.
2. Save your code from part 1. Make a copy of it with a new name and change the new code as needed to fit (in the linear least squares sense) a polynomial of order possibly lower than to a set of data , (for which the points are in no particular order). Obtain a pair of data sets of length 20 numbers , from the same URL by changing the entry in the "Number of Numbers" box. (Or if that is inaccessible, generate your own data set from random numbers added to a line.) Run your code on that data to produce the fitting coefficients when the number of coefficients of the polynomial is () (a) 1, (b) 2, (c) 3. That is: constant, linear, quadratic. Plot the fitted curves and the original data points on the same plot(s) for all three cases. Submit the following as your solution:
- Your code in a computer format that is capable of being executed.
- Your coefficients , for three cases (a), (b), (c).
- Your plot(s).
- Very brief remarks on the extent to which the coefficients are the same for the three cases.
- Can your code from this part also solve the problem of part 1?
| HEAD | NEXT |