| HEAD | PREVIOUS |
Chapter 10
Atomistic and Particle-in-Cell Simulation
When motivating the Boltzmann equation it was argued that there are too
many particles for us to track them all, so we had to use a
distribution function approach. However, for some purposes, the number
of particles that need to be tracked can in fact be managable. In that
case, we can adopt a computational modelling approach that is called
generically Atomistic Simulation. In short, it involves time-advancing
individual classical particles obeying Newton's laws of motion (or in
some relativistic cases Einstein's extensions of them).
There are also situations where it is advantageous to solve Boltmann's
equation by a method that uses
pseudo-particles, each of them representative
of a large number of individual particles. These pseudo-particles are
modelled as if they were real particles. We'll come to this broader
topic in a later section, for now just think of real particles.
10.1 Atomistic Simulation
If the particles are literally atoms or molecules, then since we will find it increasingly computationally difficult to track more than, say, a few billion of them, the volume of material that can be modelled is limited. A billion is ; so we could at most model a three-dimensional crystal lattice roughly 1000 atoms on a side. For a solid, that means the size of the region we can model is perhaps 100 nm. Nanoscale. There's no way that we are going to atomistically model a macroscopic (say 1 mm) piece of material globally with forseeable computational capacity. Still, many very interesting and important phenomena relating to solid defects, atomic displacement due to energetic particle interactions, cracking, surface behavior, and so on, occur on the 100 nm scale. Materials behavior and design is a very important area for this direct atomic or molecular simulation. The timescale in atomic interactions ranges from, say, the time it takes a gamma ray to cross a nucleus s to geological times of s. Modelling must choose a managable fraction of this enormous range, because the particle time-steps must be shorter than the fastest phenomenon to be modelled, and yet we can only afford to compute a moderate number of steps, maybe routinely as many as , but not usually , and only heroically . Phenomena outside our time-scale of choice have to be either irrelevant or represented by simplified representations of their effects in our modelling time-scale. Fig. 10.1 illustrates the computationally feasible space and time-scale region (shaded) indicating the approximate location of a few key phenomena.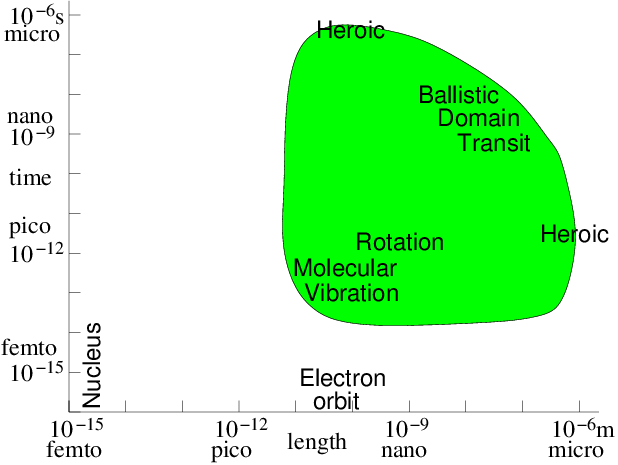
Figure 10.1: Approximate space and time scales for Molecular Dynamics
atomistic simulation of condensed matter. Molecular vibration must
be accommodated. Then computations of heroic effort are required
to explore many orders of magnitude above
it.
For materials modelling where we are considering atoms whose thermal
velocities are perhaps m/s, moving over lengths perhaps
m, the required rough time duration is s for
molecular transit. This is far longer
than the characteristic time of motion of electrons within the atoms
themselves, which is approximately the atomic size m divided
by the electron velocity at say 10eV energy m/s: a time of
s for electronic configuration. This 1 million factor
time range is too great to span routinely. So atomistic modelling
usually needs to represent the atomic physics of the electron
configurations in molecules in some averaged approximate way. This
representation can sometimes be calculated on the basis of numerical
solution of quantum mechanics, but we won't
address that aspect of the problem. On the other hand, the motions of
the atomic nuclei arising from molecular
vibrations has typical
timescale s: at least 1000 times longer than
electrons. This is managable, and indeed must be resolved, if
the dynamics of a lattice are to be modelled.

Figure 10.2: Example of a crystal lattice atomistic simulation in three
dimensions. Study of a region of nanocrystaline metal with 840,000
atoms ready to be deformed. (Courtesy: Ju Li, Massachusetts
Institute of Technology.)
Atomistic modelling therefore represents the interatomic forces
arising from
electron orbital interactions only approximately, as time
averages over electronic orbits or oscillations. But it follows the
atoms themselves in their motions in response to the interatomic
forces. The atoms are represented as classical particles interacting
via a force field. This approach is sometimes called Molecular
Dynamics. It dates from as early as
1956. A modern example is shown in Fig. 10.2.
The way a simulation works then is in outline
| 1. | Calculate the force at current position on each particle due to all the others. |
| 2. | Accelerate and move particles for , getting new velocities and positions . |
| 3. | Repeat from 1. |
where is the acceleration corresponding to position . We also usually need to store a record of where the particles go, since that is the major result of our simulation. And we need methods to analyse and visualize the large amount of data that will result: the number of steps times the number of particles times at least 6 (3 space, and 3 velocity) components.
10.1.1 Atomic/Molecular Forces and Potentials
The simplest type of forces, but still useful for a wide range of physical situations, are particle-pair attraction and repulsion. Such forces act along the vector between the particle positions, and have a magnitude that depends only upon the distance between them. An example might be the inverse-square electric force between two charges and , . But for atomistic simulation more usually neutral particles are being modelled whose force changes from mutual attraction at longer distances to mutual repulsion at short distances.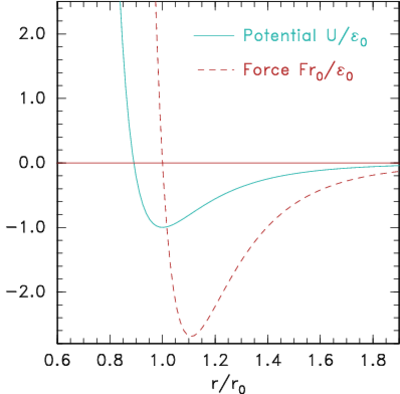 (a)
(a)
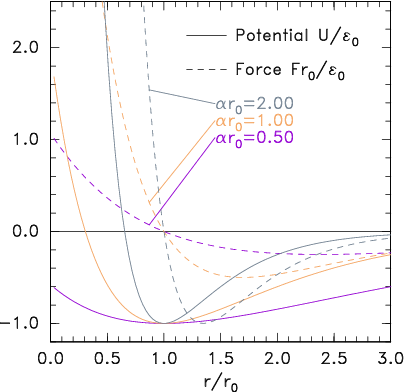 (b)
(b)
Figure 10.3: Potential and corresponding force forms for (a)
Lennard-Jones (eq. 10.2) and (b) Morse (eq. 10.3) expressions.
A very common form of interatomic
potential that gives this kind of attraction and repulsion is the
Lennard-Jones (12:6) potential (see
Fig. 10.3(a))
10.1.2 Computational requirements
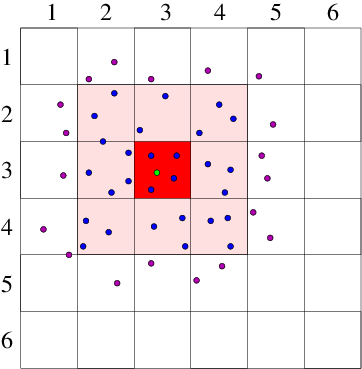
If there are particles, then to evaluate the force on particle from all the other particles , requires force evaluations for pair-forces ( term). It requires for three-particle () terms and so on. The force calculation needs to be done for all the particles at each step, so if we include even just the pair-forces for all particles, force terms must be evaluated. This is too much. For example, a million particles would require pair force evaluations per time step. Computational resources would be overwhelmed. Therefore the most important enabling simplification of a practical atomistic simulation is to reduce the number of force evaluations till it is not much worse than linear in . This can be done by taking advantage of the fact that the force laws between neutral atoms have a rather short range; so the forces can be ignored for particle spacings greater than some modest length. In reality we only need to calculate the force contributions from a moderately small number of nearby particles on each particle . It is not sufficient to look at the position of all the other particles at each step and decide whether they are near enough to worry about. That decision is itself an order cost per particle ( total). Even if it's a bit cheaper than actually evaluating the force, it won't do. Instead we have to keep track, in some possibly approximate way, of which of the other particles are close enough to the particle to matter to it. There are broadly two ways of doing this. Either we literally keep a list of near neighbors associated with each particle. Or else we divide up the volume under consideration into much smaller blocks and adopt the policy of only examining the particles in its own block and the neighboring blocks. Either of these will obviously work for a crystal lattice type problem, modelling a solid, because the atoms hardly ever change their nearest neighbors, or the members of blocks. But in liquids or gases the particles can move sufficiently that their neighbors or blocks are changing. To recalculate which particles are neighbors costs . However, there are ways to avoid having to do the neighbor determination every step. If we do it rarely enough, we reduce the cost scaling. Neighbor List Algorithm A common way to maintain an adequately accurate neighbor list is as follows. See Fig. 10.4.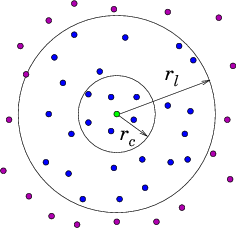 (a)
(a)
 (b)
(b)
Figure 10.4: Neighbor List (a), and Block (b), algorithms enable testing
only nearby particles for force influence. The neigbors whose
influence must be calculated are inside the radius or inside
the shaded region.
Suppose is the
cutoff radius beyond which interparticle forces are negligible. For
each particle , designate as neighbors particles within a larger
sphere . Suppose the fastest speed a
particle has is ; then we know that no particle, starting
from outside the sphere , can reach the sphere in less than
a time , that is, in fewer timesteps than
. Consequently, we need to update the
neighbor lists only every steps. The average neighbor list cost
per step is . This is smaller than , and if is large
(because the maximum velocity is small), much smaller. However, it is
still of order .
Block Algorithm
If the domain is divided into a large
number of blocks, each of which is bigger than the cutoff radius, then
we need to examine only particles that are in the same block or an
adjacent block. Adjacent blocks must be examined because a particle
near the boundary of a block might be influenced by particles just the
other side of that boundary. Suppose there are blocks. They
contain on average particles each. As the size of the
computational region increases, we can keep this ratio constant. The
total number of neighboring particles we need to examine for each
particle is (in three dimensions) Thus,
this block algorithm's step cost is , linear in the
number of particles. But the constant of proportionality might be
quite large. There is also an interesting question as to how the list
of particles in a block is maintained. One way to do this is to use a
linked list of pointers. However, such a linked list does not lend
itself readily to parallel data implementations, and there are
interesting forefront research questions as to the best practical way
of solving this problem.
10.2 Particle in Cell Codes
If the interparticle force law is of infinite range, as it is, for example, with the inverse-square interactions of charged particles in a plasma, or gravitating stars, then the near-neighbor reduction of the force calculation does not work, because there is no cutoff radius beyond which the interaction is negligible. This problem is solved in a different way, by representing the long-range interactions as the potential on a mesh of cells. This approach is called "Particle in Cell" or PIC. Consider, for simplicity, a single species of charged particles (call them electrons) of charge ( for electrons, of course), and mass . Positive ions could also be modelled as particles, but for now take them to be represented by a smooth neutralizing background of positive charge density . The electrons move in a region of space divided into cells labelled with index at positions . [Most modern PIC production codes are multidimensional, but the explanations are easier in one dimension.] They give rise to an electric potential . Ignoring the discreteness of the individual electrons, there is a smoothed-out total (sum of electron and ion) charge density . The potential satisfies Poisson's equation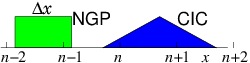 Usually a continuous linear
interpolation is preferred, called the Cloud In
Cell CIC assignment. The
charge density assigned from each electron is equal to when
the electron is exactly at , and falls linearly, reaching zero when
the particle is at . Thus the electron is like a rod of length
whose charge distribution is triangular.
The way the particle in cell code runs is this.
Usually a continuous linear
interpolation is preferred, called the Cloud In
Cell CIC assignment. The
charge density assigned from each electron is equal to when
the electron is exactly at , and falls linearly, reaching zero when
the particle is at . Thus the electron is like a rod of length
whose charge distribution is triangular.
The way the particle in cell code runs is this.
| 1. | Assign the charge from all the particles onto the grid cells. |
| 2. | Solve Poisson's equation to find the potential . |
| 3. | For each particle, find at its position, , by interpolation from the . |
| 4. | Accelerate, by the corresponding force, and move the particles. |
| 5. | Repeat from 1. |

Figure 10.6: A curved grid (relatively unusual for PIC) shaded to
represent the density normalized to the distant value.
A few representative particle orbits in the vicinity of a spherical
object are shown, and arrows indicate the mean ion
velocity.
Why introduce this cell mesh? Because this approach is computationally
far more efficient than adding up the
inverse square law forces between individual particles. An atomistic
pair-force approach costs per step. By contrast the
particle moving stage, once the force is known is . If the
potential grid has a total of points, then an efficient
iterative Poisson solution costs per step, in
dimensions, or can
be done by tridiagonal elimination in
operations in one dimension. Generally the number of
particles per cell is fairly large, so is much smaller than
and the Poisson cost scales linearly or nearly linearly with
. Therefore for practical purposes, the costs are dominantly
those of interpolating the electric field to the particle and moving
it: an order cost, not like the pair-force approach.
Sometimes the dynamics of the ions is just as important to model as
the electrons. Then the ions must be treated through the PIC approach
as a second species of particles obeying Newton's law. Actually it is
sometimes advantageous to treat only the ions this way, and treat
electrons as a continuum whose density is a known function of
. The latter approach is
often called "Hybrid" PIC.
10.2.1 Boltzmann Equation Pseudoparticle Representation
In a particle in cell code, the particles move and are tracked in phase-space: is known at each time-step. A particle's equation of motion in phase space is
Figure 10.7: Example of phase-space locations of electrons. A
one-dimensional versus calculation is illustrated, using
the code XES1 (by Birdsall, Langdon, Verboncoeur and Vahedi,
originally distributed with the text by Birdsall and Langdon) for
two streams of particles giving rise to an instability whose
wavelength is four times the domain length. Each electron position
is marked as a point. Their motion can be viewed like a
movie.
Particle in cell codes are a backbone of much computational plasma
physics, important for modelling semiconductor processing tools, space
interactions, accelerators, and fusion experiments. An example of a
one-dimensional PIC calculation is shown in Fig. 10.7. They are
particularly useful for collisionless or nearly collisionless problems
that are widespread in the field. They can also be modified to include
collisions of various different types, as the conditions require
them. In plasmas, though, charged-particle collisions are often
dominated by small scattering angles and are much better approximated
by a Fokker-Planck diffusion in phase space than by discrete events.
10.2.2 Direct Simulation Monte Carlo treatment of gas
An approach that combines some of the features of PIC and atomistic simulation, is the treatment of tenuous neutral gas behavior by what have come to be called Direct Simulation Monte Carlo (DSMC) codes. These are for addressing situations where the ratio of the mean-free-path of molecules to the characteristic spatial feature size (the "Knudsen number") is of order unity (within a factor of 100 or so either way). Such situations occur in very tenuous gases (e.g. orbital re-entry in space) or when the features are microscopic. DSMC shares with PIC the features that the domain is divided into a large number of cells, that pseudo-particles are used, and that collisions are represented in simplified way that reduces computational cost and yet approximates physical behavior. DMSC is also, in effect, integrating the Boltzmann equation along characteristics, but in this case there's no acceleration term, so the characteristics are straight lines. The pseudo-particles representing molecules are advanced in time, but at each step, chosen somewhat shorter than a typical collision time, they are examined to decide whether they have collided. In order to avoid a cost, collisions are considered only with the particles in the same cell of the grid. (This partitioning is all the cells are used for.) The cells are chosen to have size smaller than a mean-free-path, but not by much. They will generally have only a modest number (perhaps 20-40) of pseudo-particles in each cell. The number of individual molecules represented by each pseudo-particle is adjusted to achieve this number per cell. Whether a collision has occurred between two particles is decided based only upon their relative velocity, not on their position within the cell. This is the big approximation. A statistical test using random numbers decides if and which collisions have happened. A collision changes the velocity of both colliding particles, in accordance with the statistics of the collision cross-section and corresponding kinematics. That way, momentum and energy are appropriately conserved within the cell as a whole. Steps are iterated, and the overall behavior of the assembly of particles is monitored and analysed to provide effective fluid parameters like density, velocity, effective viscosity, and so on. Fig. 10.8 shows an example from the code DSMC, v3.0 developed by Graeme Bird.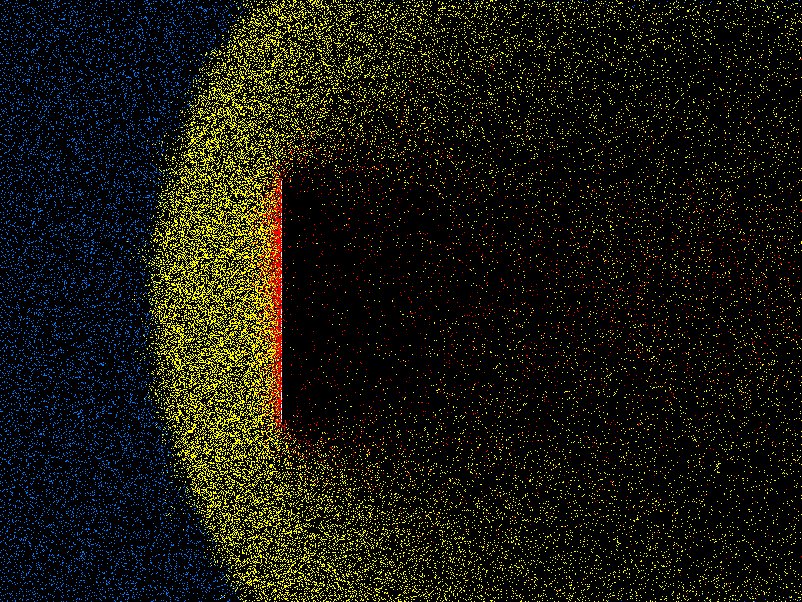
Figure 10.8: Example of position plot in two space dimensions of tenuous
gas flow past a plate. Different colors (shadings) indicate molecules that
have been influenced by the plate through collisions.
10.2.3 Particle Boundary Conditions
Objects that are embedded in a particle computation region present physical boundaries at which appropriate approximate conditions must be applied. For example with DSMC, gas particles are usually reflected, whereas with plasmas, it is usually assumed that the electrons are removed by neutralization when they encounter a solid surface. An important question arises in most particle simulation methods. What do we do at the outer boundary of our computational domain? If a particle leaves the domain, what happens to it? And what do we do to represent particles entering the domain? Occasionally the boundary of our domain might be a physical boundary no different from an embedded object. But far more often the edge of the domain is simply the place where our computation stops, not where there is any specific physical change. What do we do then? The appropriate answer depends upon the specifics of the situation, but quite often it makes sense to use periodic boundary conditions. Periodic conditions for particles are like periodic conditions for differential equations discussed in section 3.3.2. They treat the particles as if a boundary that they cross corresponds to the same position in space as the opposite boundary. A particle moving on a computational domain in that extends from to , when it steps past , to a new place that would have been , outside the domain, is reinserted at the position close to the opposite boundary, but back inside the domain. Of course the particle's velocity is just what it would have been anyway. Velocity is not affected by the reinsertion process. Periodic conditions can be applied in any number of dimensions.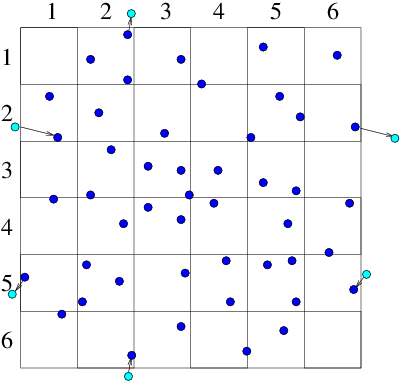 (a)
(a) (b)
(b)
Figure 10.9: Particles that cross outer periodic boundaries (a) are
relocated to the opposite side of the domain. This is equivalent (b)
to modelling an (infinite) periodic array made up of repetitions
of the smaller domain.
Periodic boundaries mean that the computation represents the phenomena
of a periodic array of domains all connected to one another and all
doing the same thing. Sometimes that is actually what one wants. But
more often it is an approximation to a larger domain. If nothing of
interest happens at a scale equal to or larger than the smaller
computational domain, then the artifically imposed periodicity is
unimportant, and the periodic conditions are a convenient way to
represent the computation of a small sub-volume within a much larger,
uniform, medium. Fig. 10.9 illustrates this point.
Sometimes, however, it is not appropriate to use periodic
conditions. In that case a particle that leaves the domain is simply
removed from the calculation. If the calculation is approximately
steady, then clearly there must also be particles created within the
domain or entering it from outside. A suitable method for
injecting them into the calculation must be implemented. It might
represent, for example, the flux of particles across the boundary from
an assumed velocity distribution function.
Worked Example: Required resolution of PIC grid
How fine must the potential mesh be in an electron Particle in Cell code?Well, it depends on how fine-scale the potential variation might be. That depends on the parameters of the particles (electrons). Suppose they have approximately a Maxwell-Boltzmann velocity-distribution of temperature . We can estimate the finest scale of potential variation as follows. We'll consider just a one-dimensional problem. Suppose there is at some position , a perturbed potential such that , measured from a chosen reference in the equilibrium background where the density is . (Referring to the background as is a helpful notation that avoids implying the value at ; it means the distant value.) Then the electron density at can be deduced from the fact that is constant along orbits (characteristics). In the collisionless steady-state, energy is conserved; so for any orbit , where is the velocity on that orbit when it is "at infinity" in the background, where . Consequently, . Hence at , is Maxwellian with density . Now let's find analytically the steady potential arising for when the potential slope at is . Poisson's equation in one-dimension is
Exercise 10. Atomistic Simulation
1. The Verlet scheme for particle advance is
Suppose that the velocity at integer timesteps is related to that at half integer timesteps by . With this identification, derive the Verlet scheme from the leap-frog scheme,
and thus show they are equivalent.
2. A block algorithm is applied to an atomistic simulation in a cubical 3 dimensional region, containing atoms approximately uniformly distributed. Only two-particle forces are to be considered. The cut-off range for particle-particle force is 4 times the average particle spacing. Find (a) The optimal size of blocks into which to divide the domain for fastest execution. (b) How many force evaluations per time-step will be required. (c) If the force evaluations require 5 multiplications, a Verlet advance is used, and the calculation is done on a single processor which takes 1 nanosecond per multiplication on average, roughly what is the total time taken per timestep (for the full 1,000,000 particles).
3. (a) Prove from the definition of a characteristic (see section 8.3.2) that the equation of the characteristics of the collisionless Boltzmann equation is
| HEAD | NEXT |