| HEAD | PREVIOUS |
Chapter 12
Monte Carlo Radiation Transport
12.1 Transport and Collisions
Consider the passage of uncharged particles through matter. The particles might be neutrons, or photons such as gamma rays. The matter might be solid, liquid, or gas, and contain multiple species with which the particles can interact in different ways. We might be interested in the penetration of the particles into the matter from the source, for example what is the particle flux at a certain place, and we might want to know the extent to which certain types of interaction with the matter have taken place, for example radiation damage or ionization. This sort of problem lends itself to modelling by Monte Carlo methods. Since the particles are uncharged, they travel in straight lines at constant speed between collisions with the matter. Actually the technique can be generalized to treat particles that experience significant forces so that their tracks are curved. However, charged particles generally experience many collisions that perturb their velocity only very slightly. Those small-angle collisions are not so easily or efficiently treated by Monte Carlo techniques, so we simplify the treatment by ignoring particle acceleration between collisions.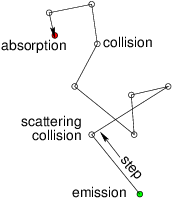
Figure 12.1: A random walk is executed by a particle with
variable-length steps between individual scatterings or
collisions. Eventually it is permanently absorbed. The statistical
distribution of the angle of
scattering is determined by the details of the collision
process.
A particle executes a random walk through the
matter, illustrated in Fig. 12.1. It travels a certain
distance in a straight line, then collides. After the collision it has
a different direction and speed. It takes another step in the new
direction, generally with a different distance, to the next
collision. Eventually the particle has an absorbing collision, or
leaves the system, or becomes so degraded (for example in energy) that
it need no-longer be tracked. The walk ends.
12.1.1 Random walk step length
The length of any of the steps between collisions is random. For any collision process, the average number of collisions a particle has per unit length corresponding to that process, which we'll label , is , where is the cross-section, and is the density in the matter of the target species that has collisions of type . For example, if the particles are neutrons and the process is uranium nuclear fission, would be the density of uranium nuclei. The average total number of collisions of all types per unit path length is therefore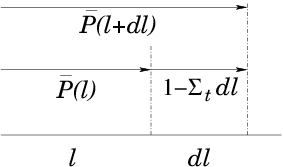
Figure 12.2: The probability, , of survival without a
collision to position decreases by a multiplicative factor
in an increment .
Therefore (refer to Fig. 12.2) if the
probability that the particle survives at least as far as without
a collision is , then the probability that it survives at
least as far as is the product of times the
probability that it does not have a collision in
:
12.1.2 Collision type and parameters
Having decided where the next collision happens, we need to decide what sort of collision it is. The local rate at which each type of collision is occuring is and the sum of all is . Therefore the fraction of collisions that is of type is .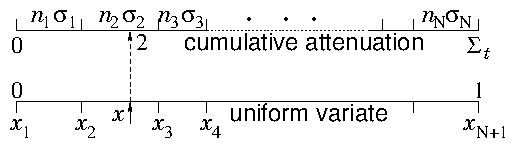 If we regard all the
possible types of collisions as arrayed in a long list, illustrated in
Fig. 12.3, and to each
type is assigned a real number such that
, i.e.
If we regard all the
possible types of collisions as arrayed in a long list, illustrated in
Fig. 12.3, and to each
type is assigned a real number such that
, i.e.
12.1.3 Iteration and New Particles
Once the collision parameters have been decided, unless the event was an absorption, the particle is restarted from the position of collision with the new velocity and the next step is calculated. If the particle is absorbed, or escapes from the modelled region, then instead we start a completely new particle. Where and how it is started depends upon the sort of radiation transport problem we are solving. If it is transport from a localized known source, then that determines the initialization position, and its direction is appropriately chosen. If the matter is emitting, new particles can be generated spread throughout the volume. Spontaneous emission, arising independent of the level of radiation in the medium, is simply a distributed source. It serves to determine the distribution of brand new particles, which are launched once all active particles have been followed till absorbed or escaped. Examples of spontaneous emission include radiation from excited atoms, spontaneous radioactive decays giving gammas, or spontaneous fissions giving neutrons. However, often the new particles are "stimulated" by collisions from the transporting particles. Fig. 12.4 illustrates this process. The classic nuclear example is induced fission producing additional neutrons. Stimulated emission arises as a product of a certain type of collision.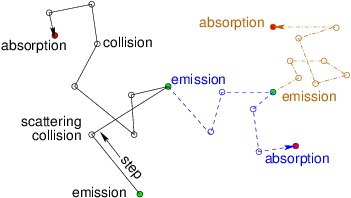
Figure 12.4: "Stimulated" emission is a source of new particles caused
by the collisions of the old ones. It can multiply the particles
through succeeding generations, as the new particles (different
line styles) give rise themselves to additional
emissions.
Any additional particles produced by collisions must be tracked by the
same process as used for the original particle. They become new
tracks. In a serial code, the secondary particles must be initialized
and then set aside during the collision step. Then when the original
track ends by absorption or escape, the code must take up the job of
tracking the secondary particles. The secondary particles may generate
tertiary particles, which will also eventually be tracked. And so on.
Parallel code might offload the secondary and tertiary tracks to other
processors (or computational threads).
One might be concerned that we'll never get to the end if particles
are generated faster than they are lost. That's true; we won't. But
particle generation faster than loss corresponds to runaway physical
situation, for example a prompt supercritical reactor. So the
real-world will have problems much more troublesome than our
computational ones!
12.2 Tracking, Tallying and Statistical Uncertainty
The purpose of a Monte Carlo simulation is generally to determine some averaged bulk parameters of the radiation particles or the matter itself. The sorts of parameters include, radiation flux as a function of position, spectrum of particle energies, rate of occurrence of certain types of collision, or resulting state of the matter through which the radiation passes. To determine these sorts of quantities requires keeping track of the passage of particles through the relevant regions of space, and of the collisions that occur there. The computational task of keeping track of events and contributions to statistical quantities is often called "tallying". What is generally done is to divide the region of interest into a managable number of discrete volumes, in which the tallies of interest are going to be accumulated. Each time an event occurs in one of these volumes, it is added to the tally. Then, provided a reasonably large number of such events has occurred, the average rate of the occurrence of events of interest can be obtained. For example, if we wish to know the fission power distribution in a nuclear reactor, we would tally the number of fission collisions occurring in each volume. Fission reactions release on average a known amount of total energy . So if the number occuring in a particular volume , during a time is , the fission power density is . The number of computational random walks that we can afford to track is usually far less than the number of events that would actually happen in the physical system being modelled. Each computational particle can be considered to represent a large number of actual particles all doing the same thing. The much smaller computational number leads to important statistical fluctuations, uncertainty, or noise, that is a purely computational limitation. The statistical uncertainty of a Monte Carlo calculation is generally determined by the observation that a sample of random choices from a distribution (population) of standard deviation has a sample mean whose standard deviation is equal to the standard error . Each tally event acts like single random choice. Therefore for tally events the uncertainty in the quantity to be determined is smaller than its intrinsic uncertainty or statistical range by a factor . Put differently, suppose the average rate of a certain type of statistically determined event is constant, giving on average events in time then the number of events in any particular time interval of length is governed by a Poisson probability, eq. (11.15) . The standard deviation of this Poisson distribution is . Therefore we obtain a precise estimate of the average rate of events, , by using the number actually observed in a particular case, , only if (and therefore ) is a large number. The first conclusion is that we must not choose our discrete tallying volumes too small. The smaller they are, the fewer events will occur in them, and, therefore, the less statistically accurate will be the estimate of the event rate. When tallying collisions, the first thought one might have is simply to put a check mark against each type of collision for each volume element, whenever that exact type of event occurs in it. The difficulty with this approach is that it will give very poor statistics, because there are going to be too few check marks. To get, say, 1% statistical uncertainty, we would need check marks for each discrete volume. If the events are spread over, say volumes, we would need total collisions of each relevant type. For, say, 100 collision types we are already up to collisions. The cost is very great. But we can do better than this naïve check-box approach. One thing we can do with negligible extra effort is to add to the tally for every type of collision, whenever any collision happens. To make this work, we must add a variable amount to the tally, not just 1 (not just a check mark). The amount we should add to each collision-type tally, is just the fraction of all collisions that is of that type, namely . Of course these fractional values should be evaluated with values of corresponding to the local volume, and at the velocity of the particle being considered (which affects ). This process will produce, on average, the same correct collision tally value, but will do so with a total number of contributions bigger by a factor equal to the number of collision types. That substantially improves the statistics.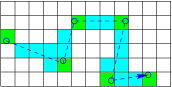
Figure 12.5: Tallying is done in discrete volumes. One can tally every
collision(green) but if the steps are larger than the
volumes, it gives better statistics to tally every volume the
particle passes through(blue).
A further statistical advantage is obtained by tallying more than just
collisions. If we want particle flux properties, as well as the
effects on the matter, we need to tally not just collisions, but also
the average flux density in all the discrete volumes. That requires us
to determine for every volume, every passage of a particle through
it, the fractional time that it spends in the volume, and
the speed at which it passed through. See Fig. 12.5. When the simulation has been tracked for a
sufficient number of particles, the density of particles in the volume
is proportional to the sum and the scalar flux
density to . If collisional lengths (the length of the random walk step) are
substantially larger than the size of the discrete volumes, then there
are more contributions to the flux property tallies than there are
walk steps, i.e. modelled collisions. The statistical accuracy of the
flux density measurement is then better than the collision tallies
(even when all collision types are tallied for every collision) by a
factor approximately equal to the ratio of collision step length to
discrete volume side-length. Therefore it may be worth the effort to
keep a tally of the total contribution to collisions of type that
we care about from every track that passes through every volume. In
other words, for each volume, to obtain the sum over all passages :
. The extra cost of this process
is the geometric task of determining the length of a line during which
it is inside a particular volume. But if that task is necessary
anyway, because flux properties are desired, then it is no more work
to tally the collisional probabilities in this way.
Importance weighting
Another aspect of statistical accuracy
relates to the choice of initial distribution of particles, especially
in velocity space. In some transport problems, it might be that the
particles that penetrate a large distance away from their source are
predominantly the high energy particles, perhaps those quite far out
on the tail of a birth velocity distribution that has the bulk of its
particles at low energy. The most straightforward way to represent the
transport problem is to launch particles in proportion to their
physical birth distribution. Each computational particle then
represents the same number of physical particles. But this choice
might mean there are very few of the high-energy particles that
determine the flux far from the source. If so, then the statistical
uncertainty of the far flux is going to be great.
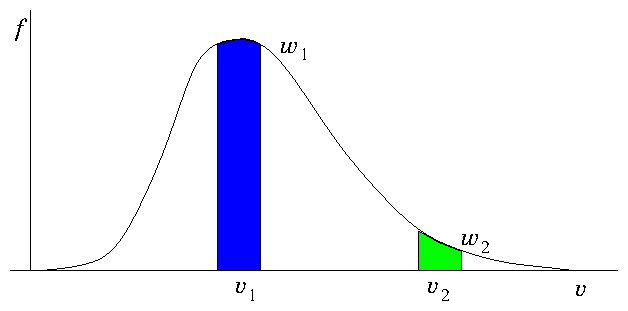
Figure 12.6: If all particles have the same weight, there are many more
representing bulk velocities () than tail velocities
(). Improved statistical representation of the tail is
obtained by giving the tail velocities lower weight . If the
weights are proportional to then equal numbers of particles
are assigned to equal velocity ranges.
It is possible to compensate for this problem by weighting the
particles, illustrated by Fig. 12.6. One can obtain
better far-flux statistics by launching more of the high energy
particles than would be implied by their probability distribution, but
compensating for the statistical excess by an importance weighting
that is inversely proportional to the factor by which the particle
number has exceeded the probability distribution. For a weighted
particle's subsequent random walk, and for any additional particles
emitted in response to collisions of the particle, the contribution
made to any flux or reaction rate is then multiplied by
. Consequently the total flux calculated anywhere has the correct
average contribution from all types of initial particles. But there
are more actual contributions (of lower weight) from
high-initial-energy particles than there otherwise would be. This has
the effect of reducing the statistical uncertainty of flux that happens
to depend upon high energy birth particles by transferring some of the
computational effort to them from lower energy birth particles.
Importance weighting is immediately accommodated during the tallying
process by adding contributions to the various flux tallies that are
the same as have been previously given - except: each contribution
is multiplied by the weight of that particular particle. Thus
density becomes and scalar flux
density , and so on.
The weight of a particle that is launched as a result of stimulated
emission is inherited from its parent. A newly launched particle of
the th generation inherently acquires the weight of the
particular previous generation particle whose collision caused the
launch. However, in the process of deciding the th generation's
initial velocity an extra launch weighting is accorded to it,
corresponding to its launch parameters; for example it might be
weighted proportional to the launch speed (or energy) probability
distribution . If so, then the weight of the newly launched
particle is
12.3 Worked Example: Density and Flux Tallies
In a Monte Carlo calculation of radiation transport from a source emitting at a fixed rate particles per second, tallies in the surrounding region are kept for every transit of a cell by every particle. The tally for density in a particular cell consists of adding the time interval during which a particle is in it, every time the cell is crossed. The tally for flux density adds up the time interval multiplied by speed: . After launching and tracking to extinction a large number of random emitted particles, the sums areDeduce quantitative physical formulas for what the particle and flux densities are (not just that they are proportional to these sums), and the uncertainties in them, giving careful rationales.
A total of particles tracked from the source (not including the other particles arising from collisions that we also had to track), is the number of particles that would be emitted in a time . Suppose the typical physical duration of a particle "flight" (the time from launch to absorption/loss of the particle and all of its descendants) is . If , then it is clear that the calculation is equivalent to treating a physical duration . In that case almost all particle flights are completed within the same physical duration . Only those that start within of the end of would be physically uncompleted; and only those that started a time less than before the start of would be still in flight when starts. The fraction affected is , which is small. But in fact, even if is not much longer than , the calculation is still equivalent to simulating a duration . In an actual duration there would then be many flights that are unfinished at the end of , and others that are part way through at its start. But on average the different types of partial flights add up to represent a number of total flights equal to . The fact that in the physical case the partial flights are of different particles, whereas in the Monte Carlo calculation they are of the same particle, does not affect the average tally. Given, then, that the calculation is effectively simulating a duration , the physical formulas for particle and flux densities in a cell of volume are
To obtain the uncertainty, we require additional sample sums. The total number of tallies in the cell of interest we'll call . We may also need the sum of the squared tally contributions and . Then finding and can be considered to be a process of making random selections of typical transits of the cell from probability distributions whose mean contribution per transit are and respectively. Of course the probability distributions aren't actually known, they are indirectly represented by the Monte Carlo calculation. But we don't need to know what the distributions are, because we can invoke the fact that the variance of the mean of a large number () of samples from a population of variance is just . We need an estimate of the population variance for density and flux density. That estimate is provided by the standard expressions for variance:
So the uncertainties in the tally sums when a fixed number of tallies occurs are
However, there is also uncertainty arising from the fact that the number of tallies is not exactly fixed, it varies from case to case in different Monte Carlo trials, each of flights. Generally is Poisson distributed, so its variance is equal to its mean . Variation in gives rise to a variation approximately in . Also it is reasonable to suppose that the variances of contribution size, and are not correlated with the variance arising from number of samples , so we can simply add them and arrive at total uncertainty in and , (which we write and )
Usually, and , in which case we can (within a factor of ) ignore the and contributions, and approximate the fractional uncertainty in both density and flux as . In this approximation, the squared sums and are unneeded.
Exercise 12. Monte Carlo Statistics
1. Suppose in a Monte Carlo transport problem there are different types of collision each of which is equally likely. Approximately what is the statistical uncertainty in the estimate of the rate of collisions of a specific type when a total of collisions has occurred (a) if for each collision just one contribution to a specific collision type is tallied, (b) if for each collision a proportionate () contribution to every collision type tally is made? If adding a tally contribution for any individual collision type has a computational cost that is a multiple times the rest of the cost of the simulation, (c) how large can be before it becomes counter-productive to add proportions to all collision type tallies for each collision?2. Consider a model transport problem represented by two particle ranges, low and high energy: . Suppose on average there are and particles in each range and is fixed. The particles in these ranges react with the material background at overall average rates and . (a) A Monte Carlo determination of the reaction rate is based on a random draw for each particle determining whether or not it has reacted during a time (chosen such that ). Estimate the fractional statistical uncertainty in the reaction rate determination after drawing and times respectively. (b) Now consider a determination using the same , , and total number of particles, , but distributed differently so that the numbers of particles (and hence number of random draws) in the two ranges are artificially adjusted to , (keeping ), and the reaction rate contributions are appropriately scaled by and . What is now the fractional statistical uncertainty in reaction rate determination? What is the optimum value of (and ) to minimize the uncertainty?
3. Build a program to sample randomly from an exponential probability distribution , using a built-in or library uniform random deviate routine. Code the ability to form a series of independent samples labelled , each sample consisting of independent random values from the distribution . The samples are to be assigned to bins depending on the sample mean . Bin contains all samples for which , where . Together they form a distribution , for that is the number of samples with in the bin . Find the mean and variance of this distribution , and compare them with the prediction of the Central Limit Theorem, for , , , and two cases: and . Submit the following as your solution:
- Your code in a computer format that is capable of being executed.
- Plots of versus , for the two cases.
- Your numerical comparison of the mean and variance, and comments as to whether it is consistent with theoretical expectations.
| HEAD | NEXT |