| HEAD | PREVIOUS |
Chapter 3
Two-point Boundary Conditions
Very
often, the boundary conditions that determine the solution of an
ordinary differential equation are applied not just at a
single value of the independent variable,
, but at two points, and . This type of problem is
inherently different from the "initial value problems" discussed previously. Initial value problems are
single-point boundary conditions. There must be more than one
condition if the system is higher order than one, but in an
initial value problem, all conditions are applied at the same place
(or time). In two-point problems we have boundary conditions at more
than one place (more than one value of the independent
variable) and we are interested in solving for the dependent
variable(s) in the interval of the independent variable.
3.1 Examples of Two-Point Problems
Many examples of two-point problems arise from steady flux conservation in the presence of sources. In electrostatics the electric potential is related to the charge density through one of the Maxwell equations: a form of Poisson's equation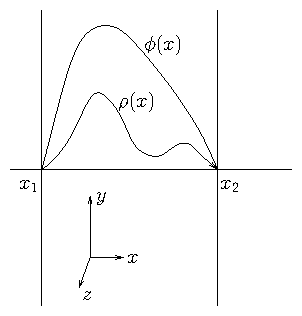
Figure 3.1: Electrostatic configuration independent of and with
conducting boundaries at and where . This is a
second-order two-point boundary problem.
In a slab geometry where varies
in a single direction (coordinate) , but not in or , an
ordinary differential equation arises
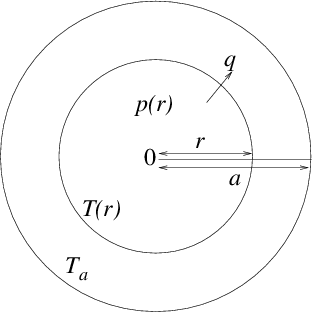
Figure 3.2: Heat balance equation in cylindrical geometry leads to a
two-point problem with conditions consisting of fixed temperature
at the edge, and zero gradient at the center .
A second-order two-point problem also arises from
steady heat conduction. See Fig. 3.2. Suppose a cylindrical reactor
fuel rod experiences volumetric heating from the nuclear reactions
inside it with a power density (Watts per cubic meter), that
varies with cylindrical radius .
Its boundary, at say, is held at a constant
temperature . If the thermal
conductivity of the
rod is , then the radial heat flux
density (Watts per
square meter) is
3.2 Shooting
3.2.1 Solving two-point problems by initial-value iteration
One approach to computing the solution to two-point problems is to use the same technique used to solve initial value problems. We treat as if it were the starting point of an initial value problem. We choose enough boundary conditions there to specify the entire solution. For a second-order equation such as (3.2) or (3.5), we would need to choose two conditions: , and , say, where and are the chosen values. Only one of these is actually the boundary condition to be applied at the initial point, . We'll suppose it is . The other, , is an arbitrary guess at the start of our solution procedure. Given these initial conditions, we can solve for over the entire range . When we have done so for this case, we can find the value at (or its derivative if the original boundary conditions there required it). Generally, this first solution will not satisfy the actual two-point boundary condition at , which we'll take as . That's because our guess of was not correct.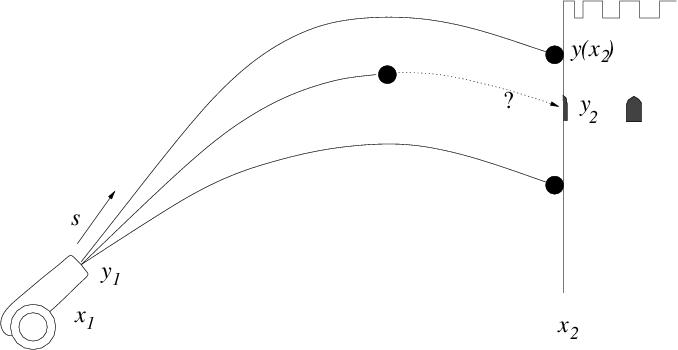
Figure 3.3: Multiple successive shots from a cannon can take advantage of
observations of where the earlier ones hit, in order to iterate the aiming
elevation until they strike the target.
It's as if we are aiming at the point with a cannon
located at (see Fig. 3.3). We elevate the
cannon so that the cannonball's initial angle is ,
which is our initial guess at the best aim. We shoot. The cannonball
flies over, (within our metaphor, the initial value solution is found)
but is not at the correct height when it reaches because our
first guess at the aim was imperfect. What do we
do? We see the height at which the cannonball hits, above or below the
target. We adjust our aim accordingly with a new elevation ,
, and shoot again. Then we
iteratively refine our aim taking as many shots as
necessary, and improving the aim each time, till we hit the target.
This is the "shooting" method of solving a two-point problem. The
cannonball's trajectory stands for the initial value integration with
assumed initial condition.
One question that is left open in this description is exactly
how we refine our aim. That is, how do we change the guess of
the initial slope so as to get a solution that is nearer to the
correct value of ? One of the easiest and most robust ways to
do this is by bisection.
3.2.2 Bisection
Suppose we have a continuous function over some interval (i.e. ), and we wish to find a solution to within that range. If and have opposite signs, then we know that there is a solution (a "root" of the equation) somewhere between and . For definiteness in our description, we'll take and . To get a better estimate of where is, we can bisect the interval and examine the value of at the point . If , then we know that a solution must be in the half interval , whereas if , then a solution must be in the other interval . We choose whichever half-interval the solution lies in, and update one or other end of our interval to be the new s-value. In other words, we set either or respectively. The new interval is half the length of the original, so it gives us a better estimate of where the solution value is.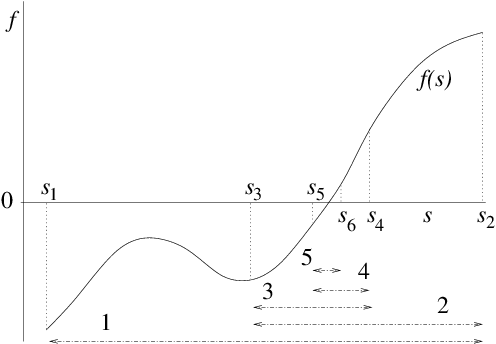
Figure 3.4: Bisection successively divides in two an interval in which there
is a root, always retaining the subinterval in which a root
lies.
Now we just iterate the above procedure, as
illustrated in Fig. 3.4. At each step we get an interval
of half the length of the previous step, in which we know a solution
lies. Eventually the interval becomes small enough that its extent can
be ignored; we then know the solution accurately enough, and can stop
the iteration.
The wonderful thing about bisection is that it highly
efficient, because it is guaranteed to converge in
"logarithmic time". If we start with an
interval of length , then at the th interation the interval
length is . So if the tolerance with which we
need the -value solution is (generally a small length),
the number of iterations we must take before
convergence is
. For
example if , then . This is a quite modest number
of iterations even for a very high degree of refinement.
There are iterative methods of root finding that converge faster than
bisection for well behaved functions. One is "Newton's
method", which may succinctly be stated as
. It converges in a
few steps when the starting guess is not too far
from the solution. Unlike bisection, it does not require two starting
points on opposite sides of the root. However, Newton's method (1)
requires derivatives of the function, which makes it more complicated
to code, (2) is less robust, because it takes big steps near
, and may even step in the wrong direction and not converge
at all in some cases. Bisection is guaranteed to converge after a
modest number of steps. Robustness is in practice
usually more important than speed.
In the context of our shooting solution of a two-point problem, the
function is the error in the boundary value at the second point
of the inital-value solution that takes
initial-value for its derivative at . The bisection generally
adjusts the initial-value until is less than some
tolerance (rather than requiring some tolerance on ).
3.3 Direct Solution
The shooting method, while sometimes useful for situations where adaptive step-length is a major benefit, is rather a back-handed way of solving two-point problems. It is very often better to solve the problem by constructing a finite difference system to represent the differential equation including its boundary conditions, and then solve that system directly.3.3.1 Second-order finite differences
First let's consider how one ought to represent a second-order derivative as finite differences. Suppose we have a uniformly spaced grid (or mesh) of values of the independent variable such that . The natural definition of the first derivative is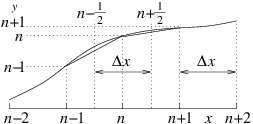
Figure 3.5: Discrete second derivative at is the difference between
the discrete derivatives at and . In a
uniform mesh, it is
divided by the same .
Because the first derivative is the value at , the second
derivative (the derivative of the first derivative) is the value at a
point mid way between and , i.e. at . Substituting
from the previous equation (3.7) we
get:
3.3.2 Boundary Conditions
However, in eq. (3.10), the top left and bottom right corners of the derivative matrix have deliberately been left ambiguous, because that's where the boundary conditions come into play. Assuming they are on the boundaries, the quantities and are determined not by the differential equation and the function , but by the boundary values. We must adjust the first and last row of the matrix accordingly to represent those boundary conditions. A convenient way to do this when the conditions consist of specifying and at the left and right-hand ends is to write the equation as: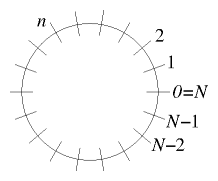
Figure 3.6: Periodic boundary conditions apply when the independent
variable is, for example, distance around a periodic domain.
A final type of boundary condition worth discussing is called
"periodic". This expression means that the end of the -domain is
considered to be connected to its beginning. Such a situation arises,
for example, if the domain is actually a circle in two-dimensional
space. But it is also sometimes used to approximate an infinite
domain. For periodic boundary conditions it is usually convenient to
label the first and last point 0 and . See Fig. 3.6. They are the same point; so
the values at and are the same. There are then
different points and the discretized differential equation must be
satisfied at them all, with the differences wrapping round to the
corresponding point across the boundary. The resulting matrix equation
is then
3.4 Conservative Differences, Finite Volumes
In our cylindrical fuel rod example, we had what one might call a "weighted derivative": something more complicated than a Laplacian. One might be tempted to write it in the following way:Worked Example: Formulating radial differences
Formulate a matrix scheme to solve by finite-differences the equationWe write down the finite difference equation at a generic position: Substituting this into the differential equation, we get
It is convenient (and improves matrix conditioning) to divide this equation through by , so that the th equation reads
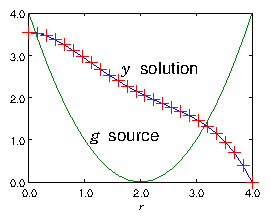
Figure 3.7: Example of the result of a finite difference solution for
of eq. (3.24) using a matrix of the form of
eq. (3.29). The source is purely
illustrative, and is plotted in the figure. The boundary points at
the ends of the range of solution are , and . A
grid size is used.
Exercise 3. Solving 2-point ODEs.
1. Write a code to solve, using matrix inversion, a 2-point ODE of the formon the -domain , spanned by an equally spaced mesh of nodes, with Dirichlet boundary conditions , . When you have got it working, obtain your personal expressions for , , , and from http://silas.psfc.mit.edu/22.15/giveassign3.cgi. (Or use , , , , , .) And solve the differential equation so posed. Plot the solution. Submit the following as your solution:
- Your code in a computer format that is capable of being executed.
- The expressions of your problem , , , and
- The numeric values of your solution .
- Your plot.
- Brief commentary ( words) on what problems you faced and how you solved them.
2. Save your code and make a copy with a new name. Edit the new code so that it solves the ODE
on the same domain and with the same boundary conditions, but with the extra parameter . Verify that your new code works correctly for small values of , yielding results close to those of the previous problem. Investigate what happens to the solution in the vicinity of . Describe what the cause of any interesting behavior is. Submit the following as your solution:
- Your code in a computer format that is capable of being executed.
- The expressions of your problem , , , and
- Brief description ( words) of the results of your investigation and your explanation.
- Back up the explanation with plots if you like.
| HEAD | NEXT |