| HEAD | PREVIOUS |
Chapter 6
Elliptic Problems and Iterative Matrix Solution
6.1 Elliptic Equations and Matrix Inversion
In elliptic equations there is no special time-like variable and no preferred direction of propagation of the physical influence. Generally, therefore elliptic equations, such as Poisson's equation, arise in solving for steady state conditions in multiple dimensions. A diffusive problem with constant (time independent) source () and boundary conditions, evolved forward in time, eventually reaches a steady state. When it has reached that state, . So the steady state satisfies the equation with the time derivative set to zero.6.2 Convergence Rate
The Gauss-Seidel method still converges nearly as slowly as the Jacobi method. The easiest way to see this (and the best way to implement the method for PDE solution) is not to update the values in increasing order of index. Instead it is better to update every other value. First update all the odd- values and then update all the even- values. The advantage is that at each stage of the update all the adjacent values in the stencil that are used have the same degree of update. The odd values are updated using the all old even values. Then the even values are updated using the all new odd values. In multiple dimensions the same effect can be achieved by updating first all the values whose indices sum to an odd value ( odd), and then those that sum to an even number. In two dimensions this choice can be illustrated by reference to a checkerboard of red and black squares representing the positions of the nodes. Fig. 6.1 illustrates the approach. The algorithm is to update first the red, then the black squares. The Red-Black updating order separates the update into two half-updates.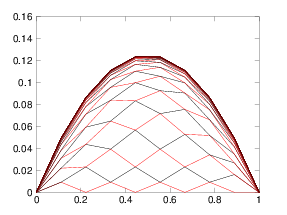 (a)
(a)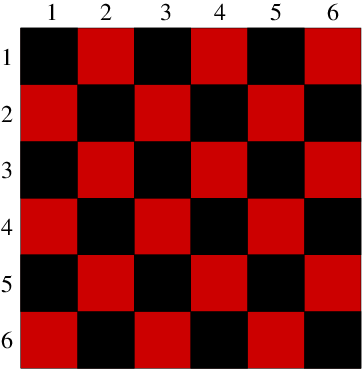 (b)
(b)
Figure 6.1: (a) One dimensional Gauss Seidel odd-even iteration produces
successive solutions for each half-step that form a web that
progresses upwards toward the solution. (b) In two dimensions the
alternate squares to be updated are all the red (lighter shaded), then all the black.
Consider a Fourier mode of wave number , where is the
integer mode number and is the length of the domain
(one-dimensional for simplicity) at whose ends Dirichlet boundary
conditions are assumed. Its half-update through eq. (6.6) (ignoring the source term), gives rise to an
amplification factor
6.3 Successive Over-Relaxation
The Gauss-Seidel method is a "successive" method where values are updated in succession, and the updated values are immediately used. It turns out that one can greatly improve the convergence rate by the simple expedient of over-correcting the error at each step. This is called "over-relaxation" and when applied to the Gauss-Seidel method is therefore called "Successive Over-Relaxation" or SOR. By analogy with eq. (6.7) it can be written- There is an optimal value of somewhere between 1 and 2, where SOR converges fastest.
- If is the amplification factor for the corresponding Jacobi iteration [ for a uniform problem] then the optimal value is .
- For this optimal the amplification factor for the SOR
is .
For the uniform case and large , these imply
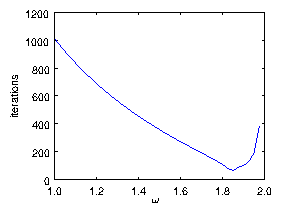
Figure 6.2: Number of iterations required to converge a SOR solution of
Poisson's equation with uniform source on a mesh of length
. It is declared converged when the maximum -change
in a step is less than . The minimum
number of iterations is found to be 63 at . This
should be compared with theoretical values of
at
.
There are other iterative matrix solution techniques, associated with
the name Krylov. Like the SOR solution technique, they
use just multiplication by the matrix, not inversion. That is a big
advantage for very sparse matrices arising in PDE solving. They go by
names like "Conjugate Gradient", "Newton
Krylov" and "GMRES". In some
situations they converge faster than SOR, and they don't require
careful adjustment of a relaxation parameter. However, they have their
own tuning problems associated with "preconditioning". These topics
are introduced very briefly in the final chapter.
6.4 Iteration and Nonlinear Equations
A major advantage accrues to iterative methods of solving elliptic problems. It is that we only have to multiply by the difference matrix. Because that difference matrix is extremely sparse, we need never in fact construct it in its entirety. We perform the matrix multiplication more physically by performing the small number of multiplications of adjacent stencil mesh values by coefficients. This saves immense amounts of storage space (compared with constructing the full matrix), and immense numbers of irrelevant multiplications by zero. The cost we must pay for the benefit of not constructing and inverting the matrix is that a substantial number of iterations is necessary. Generally for sizable multidimensional problems that iteration cost is far less than the savings. Another situation where iteration becomes essential is when the differential equations are nonlinear. In the screening of electric fields by plasmas or electrolytes, for example, the source of the Poisson equation (the charge density) is a nonlinear function of the potential, , in this case an exponential leading to:- Linearize it about the current estimate of the solution.
- Solve or advance the linear problem.
- Repeat from 1, until converged on the nonlinear solution.
6.4.1 Linearization
Suppose we have potential function , at step , not yet a solution of the steady elliptic equation. In the neighborhood of that function, we can express the source via a Taylor expansion (at each point in the mesh):6.4.2 Combining linear and nonlinear iteration
The question then arises: what method should we use to solve the linear problem to find ? It is natural to be guided by the knowledge that even if we solved the linear problem exactly, that would not give us an exact solution of the nonlinear problem. Therefore it is unnecessary to solve the linearized equation exactly. And in many cases it is in fact not even necessary to get close to the exact solution of the linearized equation for each interation of the nonlinear equation. What we then can do is to say, we'll solve the linearized equation iteratively, but we'll use only one step in our solution. In other words, is arrived at by doing a single advance of the linearized equation iterative scheme (e.g. a SOR advance). Then we recalculate and its derivative for the new value of , and iterate. Actually one might sometimes be able to dispense with the linear term in the linearization, by retaining, in the Taylor expansion for , only the first, constant term. That would amount to using as the equation to be solved for each step of the nonlinear iteration. Whether that will work depends upon the relative importance of the term in the equation. In places where is small, the nonlinear equation behaves like a transcendental equation for : simply . In that case, solving eq. (6.15), (without the term) is equivalent to a single Newton iteration of a root-finding problem, which is a sensible iteration to take. Without the linear term, though, negligibly small advance towards the nonlinear solution will occur. It is hard to generalize about how fast the iteration is going to converge on the solution of the nonlinear equation. It depends upon the type of nonlinearity. But it is usually the case that if the iterative advance is chosen reasonably, then the convergence to the nonlinear solution takes no more iterations than approximately what it would require to converge as accurately to a solution of the linearized equations. In short, iterative solutions can readily accommodate nonlinearity in the equations, and produce solutions with comparable computational cost.Worked Example: Optimal SOR relaxation
Consider the elliptic equationSuppose the final solution of the system is denoted . We can define a new dependent variable , which is the error between some approximation of the solution () and the actual solution. Of course, while we are in the process of finding the solution, we don't know how to derive from , because we don't yet know what is. That fact does not affect the following arguments. Substituting for in the differential equation and using the fact that exactly satisfies it and the boundary conditions, we immediately deduce that satisfies the homogeneous differential equation
For brevity in the rest of our equations, let's define a number to represent the second term
The resulting amplification factor for SOR iteration using this is
Collecting terms together
which can be written
The eigenvalues of the advancing matrix are the "amplification factors" for the true modes of the system. They are the solutions, , of . But
So
Now the determinant of any matrix , where and are lower and upper triangular parts and is the diagonal, is independent of . One can see this by noticing that any term in the expansion of the determinant has equal numbers of elements from as it has from ; so the factors cancel out. As implied by our notation, we can arrange the nodes in an appropriate order such that all the even coefficients are in the upper triangle and the odd coefficients in the lower triangle part of the matrix. This would be achieved by the simple expedient of putting all the even positions first. Actually we don't need to do the rearrangement. We just need to know it could be done. In that case, we can balance the upper and lower parts of the determinantal equation, multiplying the term by and the term by to make it:
i.e.
Now notice that the eigenvalues for the Jacobi iteration matrix, , satisfy , which is exactly the same equation with the identification . There's a direct mapping between eigenvalues of the Jacobi iteration and of the SOR iteration. The relationship can be considered a quadratic equation for , given and
The optimum gives the smallest magnitude of the larger solution. It occurs when the roots coincide, i.e. when whose solution is
The corresponding eigenvalue is . For , the roots for are complex with magnitude . Therefore SOR is stable only for , and the convergence rate degrades linearly to zero between and 2.
Exercise 6. Iterative Solution of Matrix Problems.
1. Start with your code that solved the diffusion equation explicitly. Adjust it to always take timesteps at the stability limit , so that:
Now it is a Jacobi iterator for solving the steady-state elliptic matrix equation. Implement a convergence test that finds the maximum absolute change in and divides it by the maximum absolute , giving the normalized -change. Consider the iteration to be converged when the normalized -change is less than (say) . Use it to solve
on the domain with boundary conditions , with a total of equally-spaced nodes. Find how many iterations it takes to converge, starting from an initial state , when (a) (b) (c) Compare the number of iterations you require with the analytic estimate in the notes. How good is the estimate? Now we want to check how accurate the solution really is. (d) Solve the equation analytically, and find the value of at , . (e) For the three values, find the relative error in . (f) Is the actual relative error the same as the convergence test value ? Why?
2. Optional and not for credit. Turn your iterator into a SOR solver by splitting the iteration matrices up into red and black (odd and even) advancing parts. Each part-iterator then uses the latest values of , that has just been updated by the other part-iterator. Also provide yourself an over-relaxation parameter . Explore how fast the iterations converge as a function of and .
Note. Although in Octave/Matlab it is convenient to implement the matrix multiplications of the advance using a literal multiplication by a big sparse matrix, one does not do that in practice. There are far more efficient ways of doing the multiplication, that avoid all the irrelevant multiplications by zero.
| HEAD | NEXT |