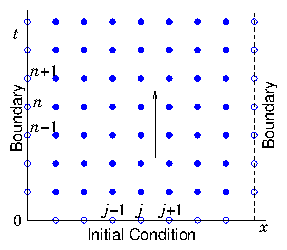
| HEAD | PREVIOUS |
| (5.1) |
| (5.2) |
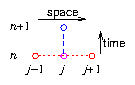
| (5.3) |
| (5.4) |
| (5.5) |
| (5.6) |
| (5.7) |
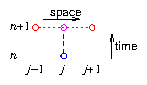 We'll see a little later how to actually solve this
equation for the values at n+1, but we can do the same stability
analysis on it without knowing. The combination for the spatial
Fourier mode is just as in eq. (5.4), so the update
equation (ignoring S) for a Fourier mode is
We'll see a little later how to actually solve this
equation for the values at n+1, but we can do the same stability
analysis on it without knowing. The combination for the spatial
Fourier mode is just as in eq. (5.4), so the update
equation (ignoring S) for a Fourier mode is
| (5.8) |
|
| (5.10) |
| (5.11) |
| (5.12) |
| (5.13) |
| (5.14) |
| (5.15) |
| (5.16) |
| (5.17) |
| (5.18) |
| (5.19) |
|
∂ψ
| =0 |
|
| (5.21) |
| (5.22) |
|
∂ψ
| =0 |
| (1+ |
∆r
| )2(ψ2,l−ψ1,l)/∆r2=4(ψ2,l−ψ1,l)/∆r2 |
| (5.23) |
| (5.24) |
|
|
|
|
| HEAD | NEXT |