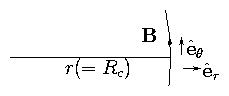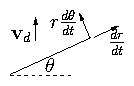HEAD

Chapter 2
Motion of Charged Particles in Fields

Plasmas are complicated because motions of electrons and ions are determined by the electric and magnetic fields but also change the fields by the currents they carry.

For now we shall ignore the second part of the problem and assume that Fields are Prescribed.

Even so, calculating the motion of a charged particle can be quite hard.

Equation of motion:

Rate of change of momentum

q
charge

(

E
E−field

v
velocity

∧

B
B−field

)

Lorentz Force

(2.1)

Have to solve this differential equation, to get position r and velocity (v= · r) given E(r,t), B(r,t).

Approach here: Start simple, gradually generalize. For a more sophisticated demonstration that the simple results are comprehensive see http://silas.psfc.mit.edu/introplasma/drifts.pdf.

2.1 Uniform B field, E = 0.

⋅

= q v∧B

(2.2)

2.1.1 Qualitatively

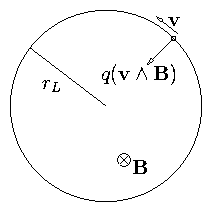
in the plane perpendicular to B:

Figure 2.1: Circular orbit in uniform magnetic field.

Accel. is perp to v so particle moves in a circle whose radius r_L is such as to satisfy

m r_L Ω² = m

v_⊥²

r_L

= |q |v_⊥ B

(2.3)

Ω is the angular (velocity) frequency

1st equality shows Ω² = v_⊥² /r_L² (r_L = v_⊥ / Ω)

Hence second gives m v_⊥ Ω = |q |v_⊥ B

i.e. Ω =

|q |B

(2.4)

Particle moves in a circular orbit with

angular frequency Ω =

|q |B

the "Cyclotron Frequency"

(2.5)

and radius r_l =

v_⊥

Ω

the "Larmor Radius.

(2.6)

2.1.2 By Vector Algebra

Particle Energy is constant. proof: take v. Eq. of motion then

m v.
⋅

v

= d
dt
⎛
⎝ 1
2
m v² ⎞
⎠ = q v. (v∧B) = 0 .
(2.7)
Parallel and Perpendicular motions separate. v_|| = constant because accel ( ∝ v∧B) is perpendicular to B.

Perpendicular Dynamics:

Take B in ∧z direction and write components

⋅

= q v_y B , m

⋅

= − q v_x B

(2.8)

Hence

⋅⋅

⋅

= −

⎛
⎝

⎞
⎠

v_x = − Ω² v_x

(2.9)

Solution: v_x = v_⊥ cosΩt (choose zero of time)

Substitute back:

v_y =

⋅

= −

|q |

v_⊥ sinΩt

(2.10)

Integrate:

x = x₀ +

v_⊥

Ω

sinΩt , y = y₀ +

|q |

v_⊥

Ω

cosΩt

(2.11)

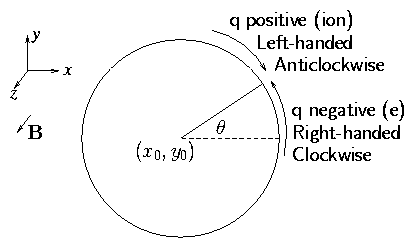
Figure 2.2: Gyro center (x₀,y₀) and orbit projection viewed from positive z.

This is the equation of a circle with center r₀ = (x₀, y₀) and radius r_L = v_⊥/ Ω: Gyro Radius. [Angle is θ = Ωt]

Direction of rotation is as indicated in Fig. 2.2 for opposite sign of charge:

Ions rotate anticlockwise. Electrons clockwise about the magnetic field.

The current carried by the plasma always is in such a direction as to reduce the magnetic field.

This is the property of a magnetic material which is "Diamagnetic".

When v_|| is non-zero the total motion is along a helix.

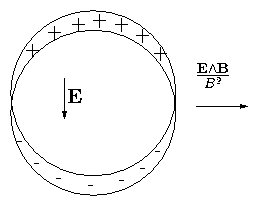
2.2 Uniform B and non-zero E

⋅

= q (E+ v∧B)

(2.12)

Parallel motion: Before, when E = 0 this was v_|| = const. Now it is clearly

⋅

q E_||

(2.13)

Constant acceleration along the field.

Perpendicular Motion

Qualitatively:

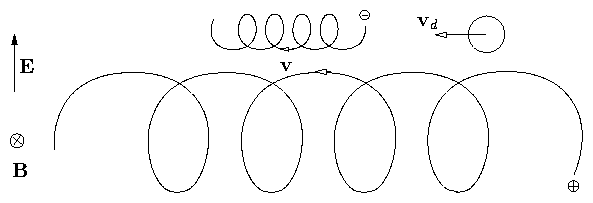
Figure 2.3: E∧B drift orbit

Speed of positive particle is greater at top than bottom so radius of curvature is greater. See Fig. 2.3. Result is that guiding center moves perpendicular to both E and B. It `drifts' across the field.

Algebraically: It is clear that if we can find a constant velocity v_d that satisfies

E+ v_d ∧B= 0

(2.14)

then the sum of this drift velocity plus the velocity

v_L =

[r_L e^{iΩ(t−t₀)}]

(2.15)

which we calculated for the E = 0 gyration will satisfy the equation of motion.

Take ∧B the above equation:

0 = E∧B+ (v_d ∧B) ∧B=E∧B+ (v_d . B) B− B² v_d

(2.16)

so that

v_d =

E∧B

B²

(2.17)

does satisfy it.

Hence the full solution is

v_||
parallel

v_d
cross−field drift

v_L
Gyration

(2.18)

where

⋅

q E_||

(2.19)

and

v_d (eq 2.17) is the "E × B drift" of the gyrocenter.

Comments on E × B drift:

It is independent of the properties of the drifting particle (q, m, v, whatever).
Hence it is in the same direction for electrons and ions.
Underlying physics for this is that in the frame moving at the E × B drift E = 0. We have `transformed away' the electric field.
Formula given above is exact except for the fact that relativistic effects have been ignored. They would be important if v_d ∼ c.

2.2.1 Drift due to Gravity or other Forces

Suppose particle is subject to some other force, such as gravity. Write it F so that

⋅

= F + q v∧B = q (

F+ v∧B)

(2.20)

This is just like the Electric field case except with F/q replacing E.

The drift is therefore

v_d =

F ∧B

B²

(2.21)

In this case, if force on electrons and ions is same, they drift in opposite directions.

This general formula can be used to get the drift velocity in some other cases of interest (see later).

2.3 Non-Uniform B Field

If B-lines are straight but the magnitude of B varies in space we get orbits that look qualitatively similar to the E ⊥ B case:

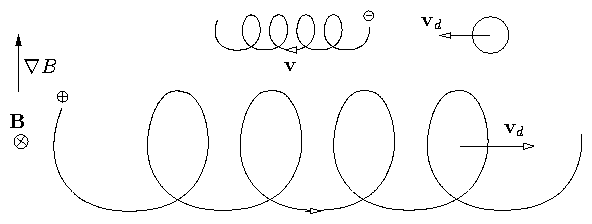
Figure 2.4: ∇B drift orbit

Curvature of orbit is greater where B is greater causing loop to be small on that side. Result is a drift perpendicular to both B and ∇B. Notice, though, that electrons and ions go in opposite directions (unlike E∧B).

Algebra

We try to find a decomposition of the velocity as before into v = v_d + v_L where v_d is constant.

We shall find that this can be done only approximately. Also we must have a simple expression for B. This we get by assuming that the Larmor radius is much smaller than the scale length of B variation i.e.,

r_L << B/ |∇ B |

(2.22)

in which case we can express the field approximately as the first two terms in a Taylor expansion:

B ≅ B₀ + (r. ∇ ) B

(2.23)

Then substituting the decomposed velocity we get:

⋅

= q (v∧B) = q [ v_L ∧B₀ + v_d ∧B₀ + (v_L + v_d) ∧(r. ∇) B]

(2.24)

or 0

v_d ∧B₀ + v_L ∧(r. ∇ ) B+ v_d ∧(r. ∇) B

(2.25)

Now we shall find that v_d/v_L is also small, like r| ∇B | /B. Therefore the last term here is second order but the first two are first order. So we drop the last term.

Now the awkward part is that v_L and r_L are periodic. Substitute r = r_c + r_L where r_c is the center of the orbit (gyrocenter), the nonperiodic part; then

0 = v_d ∧B₀ + v_L ∧(r_L . ∇ ) B+ v_L ∧( r_c . ∇ ) B

(2.26)

We now average over a cyclotron period. The last term is ∝ e^−iΩt so it averages to zero:

0 = v_d ∧B+ 〈v_L ∧(r_L . ∇ ) B〉 .

(2.27)

To perform the average use

r_L = ( x_L , y_L)

v_⊥

Ω

⎛
⎝

sinΩt ,

|q |

cosΩt

⎞
⎠

(2.28)

v_L = (

⋅

)

v_⊥

⎛
⎝

cosΩt ,

−q

|q |

sinΩt

⎞
⎠

(2.29)

So [ v_L ∧(r. ∇ ) B]_x

v_y y

(2.30)

[ v_L ∧( r. ∇ ) B]_y

−v_x y

(2.31)

taking ∇B to be in the y-direction.

Then

〈v_y y 〉

− 〈cosΩt sinΩt 〉

v_⊥²

Ω

= 0

(2.32)

〈v_x y 〉

|q |

〈cosΩt cosΩt 〉

v_⊥²

Ω

v_⊥²

Ω

|q |

(2.33)

〈v_L ∧(r. ∇ ) B〉 = −

|q |

v_⊥²

Ω

∇ B

(2.34)

Substitute in:

0 = v_d ∧B−

|q |

v_⊥²

2Ω

∇ B

(2.35)

and solve as before to get

v_d =

⎛
⎝

−q

|q |

v_⊥²

2 Ω

∇ B

⎞
⎠

∧B

B²

|q |

v_⊥²

2 Ω

B∧∇ B

B²

(2.36)

or equivalently

v_d =

mv_⊥²

2 B

B∧∇ B

B²

(2.37)

This is called the `Grad B drift'.

2.4 Curvature Drift

When the B-field lines are curved and the particle has a velocity v_|| along the field, another drift occurs.

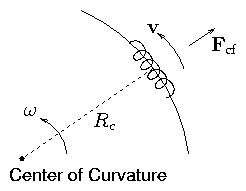
Figure 2.5: Curvature and Centrifugal Force

Take |B| constant; radius of curvature R_c.

To 1st order the particle just spirals along the field.

In the frame of the guiding center a force appears because the plasma is rotating about the center of curvature.

This centrifugal force is F_cf

F_cf = m

v_||²

R_c

pointing outward

(2.38)

as a vector

F_cf = m v_||²

R_c

R_c²

(2.39)

[There is also a coriolis force 2m(ω ∧v) but this averages to zero over a gyroperiod.]

Use the previous formula for a force

v_d =

F_cf ∧B

B²

m v_||²

q B²

R_c ∧B

R_c²

(2.40)

This is the "Curvature Drift".

It is often convenient to have this expressed in terms of the field gradients. So we relate R_c to ∇B etc. as follows:

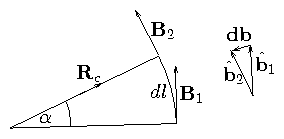
Figure 2.6: Differential expression of curvature

(Carets denote unit vectors)

From the diagram

db =

−

= −

(2.41)

and

d l = αR_c

(2.42)

d b

d l

= −

R_c

= −

R_c

R_c²

(2.43)

But (by definition)

d b

d l

= (

. ∇ )

(2.44)

So the curvature drift can be written

v_d =

m v_||²

R_c

R_c²

∧

B²

mv_||²

B∧(

. ∇ )

B²

(2.45)

2.4.1 Vacuum Fields

Relation between ∇ B & R_c drifts

The curvature and ∇B are related because of Maxwell's equations, their relation depends on the current density j. A particular case of interest is j=0: vacuum fields.

Figure 2.7: Local polar coordinates in a vacuum field

∇ ∧B= 0 (static case)

(2.46)

Consider the z-component

0 = ( ∇ ∧B)_z

∂

∂r

(r B_θ ) (B_r = 0 by choice).

(2.47)

∂B_θ

∂r

B_θ

(2.48)

or, in other words,

( ∇ B )_r = −

R_c

(2.49)

[Note also 0 = (∇ ∧B)_θ = ∂B_θ/∂z : (∇ B )_z = 0]

and hence (∇ B)_perp = − B R_c/R_c².

Thus the grad B drift can be written:

v_∇B =

mv_⊥²

2 q

B∧∇ B

B³

mv_⊥²

2 q

R_c ∧B

R_c² B²

(2.50)

and the total drift across a vacuum field becomes

v_R + v_∇B =

⎛
⎝

mv_||² +

mv_⊥²

⎞
⎠

R_c ∧B

R_c² B²

(2.51)

Notice the following:

R_c & ∇B drifts are in the same direction.
They are in opposite directions for opposite charges.
They are proportional to particle energies
Curvature ↔ Parallel Energy (× 2)
∇B ↔ Perpendicular Energy
As a result one can very quickly calculate the average drift over a thermal distribution of particles because

〈 1
2
m v_||² 〉

=

T
2

(2.52)

〈 1
2
m v_⊥² 〉

=

T 2 degrees of freedom
(2.53)

Therefore

〈v_R + v_∇B 〉 = 2T
q
R_c ∧B
R_c² B²
⎛
⎜
⎝ = 2T
q

B∧ ⎛
⎝
^

b

. ∇ ⎞
⎠
^

b

B²
⎞
⎟
⎠
(2.54)

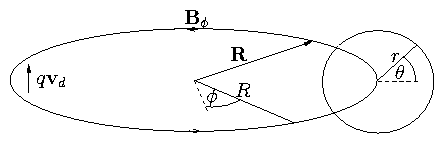
2.5 Interlude: Toroidal Confinement of Single Particles

Since particles can move freely along a magnetic field even if not across it, we cannot obviously confine the particles in a straight magnetic field. Obvious idea: bend the field lines into circles so that they have no ends.

Figure 2.8: Toroidal field geometry

Problem

Curvature & ∇B drifts

v_d

⎛
⎝

mv_||² +

mv_⊥²

⎞
⎠

R ∧B

R² B²

(2.55)

|v_d |

⎛
⎝

mv_||² +

mv_⊥²

⎞
⎠

(2.56)

Figure 2.9: Charge separation due to vertical drift

Ions drift up. Electrons down. There is no confinement. When there is finite density things are even worse because charge separation occurs → E → E ∧B → Outward Motion.

2.5.1 How to solve this problem?

Consider a beam of electrons v_|| ≠ 0 v_⊥ = 0. Drift is

v_d =

mv_||²

B_TR

(2.57)

What B_z is required to cancel this?

Adding B_z gives a compensating vertical velocity

v = v_||

B_z

B_T

for B_z << B_T

(2.58)

We want total

v_z = 0 = v_||

B_z

B_T

mv_||²

B_TR

(2.59)

So B_z = − mv_||/ Rq is the right amount of field.

Note that this is such as to make

r_L (B_z) =

|mv_|| |

|q B_z |

= R .

(2.60)

But B_z required depends on v_|| and q so we can't compensate for all particles simultaneously.

Vertical field alone cannot do it.

2.5.2 The Solution: Rotational Transform

Figure 2.10: Tokamak field lines with rotational transform

Toroidal Coordinate system (r, θ, ϕ) (minor radius, poloidal angle, toroidal angle), see figure 2.8.

Suppose we have a poloidal field B_θ

Field Lines become helical and wind around the torus: figure 2.10.

In the poloidal cross-section the field describes a circle as it goes round in ϕ.

Equation of motion of a particle exactly following the field is:

d θ

B_θ

B_ϕ

v_ϕ =

B_θ

B_ϕ

v_|| =

B_θ

v_||

(2.61)

and

r = constant.

(2.62)

Now add on to this motion the cross field drift in the ∧z direction.

Figure 2.11: Components of velocity

d θ

B_θ

v_|| + v_d cosθ

(2.63)

v_d sinθ

(2.64)

Take ratio, to eliminate time:

dθ

v_d sinθ

B_θ

v_|| +v_d cosθ

(2.65)

Take B_θ, B, v_||, v_d to be constants, then we can integrate this orbit equation:

[ lnr ] = [ − ln|

B_θ v_||

+ v_d cosθ|] .

(2.66)

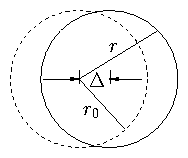
Take r = r₀ when cosθ = 0 (θ = [( π)/2]) then

r = r₀ /

⎡
⎣

1 +

Bv_d

B_θ v_||

cosθ

⎤
⎦

(2.67)

If [( Bv_d)/(B_θ v_|| )] << 1 this is approximately

r = r₀ − ∆cosθ

(2.68)

where ∆ = [(Bv_d)/(B_θ v_|| )] r₀

This is approximately a circular orbit shifted by a distance ∆:

Figure 2.12: Shifted, approximately circular orbit

Substitute for v_d

∆

≅

r₀

B_θ

(mv_||² +

mv_⊥²)

v_||

B_ϕ R

(2.69)

≅

q B_θ

mv_||² +

mv_⊥²

v_||

r₀

(2.70)

If v_⊥ = 0

∆ =

mv_||

q B_θ

r₀

= r_Lθ

r₀

(2.71)

where r_Lθ is the Larmor Radius in a field B_θ ×r / R.

Provided ∆ is small, particles will be confined. Obviously the important thing is the poloidal rotation of the field lines: Rotational Transform.

Rotational Transform

rotational transform

≡

poloidal angle

1 toroidal rotation

(2.72)

( transform / 2π = )

ι ≡

poloidal angle

toroidal angle

(2.73)

(Originally, ι was used to denote the transform. Since about 1990 it has been used to denote the transform divided by 2π which is the inverse of the safety factor.)

`Safety Factor'

q_s =

toroidal angle

poloidal angle

(2.74)

Actually the value of these ratios may vary as one moves around the magnetic field. Definition strictly requires one should take the limit of a large no. of rotations.

q_s is a topological number: number of rotations the long way per rotation the short way.

Cylindrical approx.:

q_s =

r B_ϕ

R B_θ

(2.75)

In terms of safety factor the orbit shift can be written

|∆| = r_{L θ}

= r_{L ϕ}

B_ϕ r

B_θ R

= r_L q_s

(2.76)

(assuming B_ϕ >> B_θ).

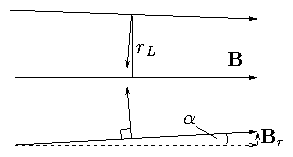
2.6 The Mirror Effect of Parallel Field Gradients: E = 0, ∇B ||B

Figure 2.13: Basis of parallel mirror force

In the above situation there is a net force along B.

Force is

< F_|| >

− |q v∧B| sinα = − |q |v_⊥ B sinα

(2.77)

sinα

− B_r

(2.78)

Calculate B_r as function of B_z from ∇ . B = 0.

∇ . B=

∂

∂r

(rB_r) +

∂

∂z

B_z = 0 .

(2.79)

Hence

[rB_r] = −

⌠
⌡

∂B_z

∂z

(2.80)

Suppose r_L is small enough that [(∂B_z)/(∂z)] ≅ const.

[ r B_r]₀^r_L ≅ −

⌠
⌡

r_L

0

r dr

∂B_z

∂z

= −

r_L²

∂B_z

∂z

(2.81)

B_r(r_L) = −

r_L

∂B_z

∂z

(2.82)

sinα = −

B_r

= +

r_L

∂B_z

∂z

(2.83)

Hence

< F_|| > = − |q |

v_⊥ r_L

∂B_z

∂z

= −

mv_⊥²

∂B_z

∂z

(2.84)

As particle enters increasing field region it experiences a net parallel retarding force.

Define Magnetic Moment

μ ≡

m v_⊥² / B .

(2.85)

Note this is consistent with loop current definition

μ = A I = πr_L² .

|q |v_⊥

2 πr_L

|q |r_L v_⊥

(2.86)

Force is F_|| = μ . ∇_|| B

This is force on a `magnetic dipole' of moment μ.

F_|| = μ . ∇_|| B

(2.87)

Our μ always points along B but in opposite direction.

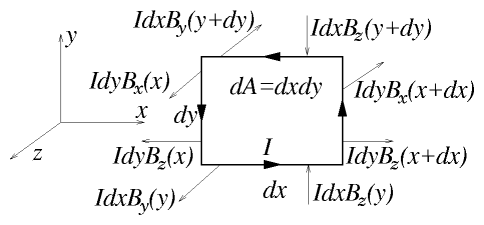
2.6.1 Force on an Elementary Magnetic Moment Circuit

Figure 2.14: Force components on an elementary circuit constituting a magnetic dipole.

Consider a plane rectangular circuit carrying current I having elementary area dxdy = dA. Regard this as a vector pointing in the z direction dA. The force on this circuit in a field B(r) is F such that

F_x

Idy [B_z (x+dx) − B_z(x)] = I dydx

∂B_z

∂x

(2.88)

F_y

−I dx [B_z (y+dy) − B_z(y)] = I dydx

∂B_z

∂y

(2.89)

F_z

− I dx [B_y (y+dy) − B_y(y)] − I dy[B_x(x+dx) − B_x(x)]

(2.90)

− I dxdy

⎡
⎣

∂B_x

∂x

∂B_y

∂y

⎤
⎦

= I dydx

∂B_z

∂z

(2.91)

(Using ∇ . B = 0).

Hence, summarizing: F = I dydx ∇ B_z. Now define μ = I dA = I dydx ∧z and take it constant. Then clearly the force can be written

F = ∇ (B. μ ) [ Strictly = (∇ B) . μ]

(2.92)

μ is the (vector) magnetic moment of the circuit.

The shape of the circuit does not matter since any circuit can be considered to be composed of the sum of many rectangular circuits. So in general

μ = I dA

(2.93)

and force is

F = ∇ (B. μ) (μ constant),

(2.94)

We shall show in a moment that |μ | is constant for a circulating particle, regarded as an elementary circuit. Also, μ for a particle always points in the -B direction. [Note that this means that the effect of particles on the field is to decrease it.] Hence the force may be written

F = − μ∇ B

(2.95)

This gives us both:

Magnetic Mirror Force:

F_|| = −μ∇_||B
(2.96)
and
Grad B Drift:

v_∇B = 1
q
F ∧B
B²
= μ
q
B∧∇ B
B²
.
(2.97)

2.6.2 μ is a constant of the motion

`Adiabatic Invariant'

Proof from F_||

Parallel equation of motion

dv_||

= F_|| = − μ

(2.98)

m v_||

dv_||

(

m v_||² ) = − μv_z

= − μ

(2.99)

(

m v_||²) + μ

= 0 .

(2.100)

Conservation of Total KE

(

mv_||² +

mv_⊥² ) = 0

(2.101)

(

mv_||² + μB) = 0

(2.102)

Combine

(μB) − μ

= 0

(2.103)

d μ

= 0 As required

(2.104)

Angular Momentum

of particle about the guiding center is

r_L mv_⊥

mv_⊥

|q |B

m v_⊥ =

|q |

mv_⊥²

(2.105)

|q |

μ .

(2.106)

Conservation of magnetic moment is basically conservation of angular momentum about the guiding center.

Proof direct from Angular Momentum

Consider angular momentum about G.C. Because θ is ignorable (locally) Canonical angular momentum is conserved.

p = [ r ∧( m v+ q A) ]_z conserved.

(2.107)

Here A is the vector potential such that B = ∇ ∧A

the definition of the vector potential means that

B_z

∂(rA_θ))

∂r

(2.108)

⇒ r_L A_θ (r_L)

⌠
⌡

r_L

0

r . B_z dr =

r_L²

B_z =

μm

|q |

(2.109)

Hence

− q

|q |

r_L v_⊥ m + q

mμ

|q|

(2.110)

−

|q |

m μ.

(2.111)

So p = const ↔ μ = constant.

Conservation of μ is basically conservation of angular momentum of particle about G.C.

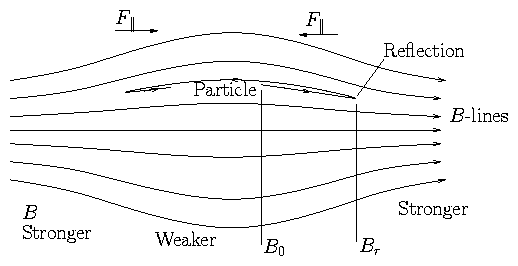
2.6.3 Mirror Trapping

Figure 2.15: Magnetic Mirror

F_|| may be enough to reflect particles back. But may not!

Let's calculate whether it will:

Suppose reflection occurs.

At reflection point v_||r = 0.

Energy conservation

m (v_⊥0² + v_||0²) =

m v_⊥r²

(2.112)

μ conservation

m v_⊥0²

B₀

m v_⊥r²

B_r

(2.113)

Hence

v_⊥0² + v_||0²

B_r

B₀

v_⊥0²

(2.114)

B₀

B_r

v_⊥0²

v_⊥0² + v_||o²

(2.115)

Pitch Angle θ

tanθ

v_⊥

v_||

(2.116)

B₀

B_r

v_⊥0²

v_⊥0² +v_||0²

= sin² θ₀

(2.117)

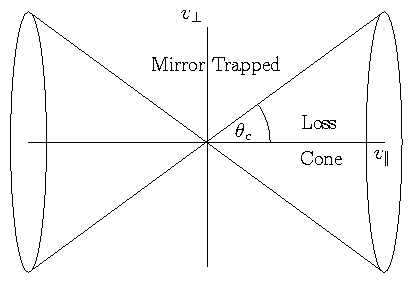
So, given a pitch angle θ₀, reflection takes place where B₀/B_r = sin²θ₀.

If θ₀ is too small no reflection can occur.

Critical angle θ_c is obviously

θ_c = sin⁻¹ (B₀ / B₁)^¹/₂

(2.118)

Loss Cone is all θ < θ_c.

Figure 2.16: Critical angle θ_c divides velocity space into a loss-cone and a region of mirror-trapping

Importance of Mirror Ratio: R_m = B₁ / B₀.

2.6.4 Other Features of Mirror Motions

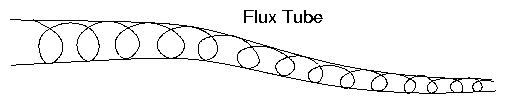
Flux enclosed by gyro orbit is constant.

πr_L² B =

πm² v_⊥²

q² B²

(2.119)

2 πm

q²

mv_⊥²

(2.120)

2 πm

q²

μ = constant.

(2.121)

Figure 2.17: Flux tube described by orbit

Note that if B changes `suddenly' μ might not be conserved.

Basic requirement

r_L << B / |∇B |

(2.122)

Slow variation of B (relative to r_L).

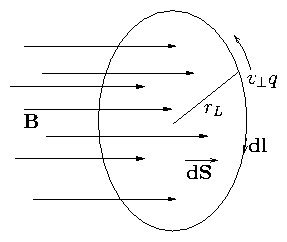
2.7 Time Varying B Field (E inductive)

Figure 2.18: Particle orbits round B so as to perform a line integral of the Electric field

Particle can gain energy from the inductive E field

∇∧E

−

∂B

∂t

(2.123)

⌠
(⎜)
⌡

E. d l

−

⌠
⌡

⋅

. ds = −

d Φ

d t

(2.124)

Hence work done on particle in 1 revolution is

δw = −

⌠
(⎜)
⌡

|q|E. dl = + |q |

⌠
⌡

⋅

. ds = + |q |

d Φ

= |q |

⋅

πr_L²

(2.125)

(dl and v_⊥ q are in opposition directions).

⎛
⎝

m v_⊥²

⎞
⎠

|q |

⋅

πr _L² =

2 π

⋅

|q |B

m v_⊥²

(2.126)

2 π

⋅

|Ω|

μ.

(2.127)

Hence

⎛
⎝

m v_⊥²

⎞
⎠

|Ω|

2 π

⎛
⎝

mv_⊥²

⎞
⎠

= μ

(2.128)

but also

⎛
⎝

mv_⊥²

⎞
⎠

( μB ) .

(2.129)

Hence

dμ

= 0 .

(2.130)

Notice that since Φ = [(2 πm)/(q² )] μ, this is just another way of saying that the flux through the gyro orbit is conserved.

Notice also energy increase. Method of `heating'. Adiabatic Compression.

2.8 Time Varying E-field (E, B uniform)

Recall the E∧B drift:

v_{E ∧B} =

E∧B

B²

(2.131)

when E varies so does v_{E ∧B}. Thus the guiding centre experiences an acceleration

⋅

E ∧B

⎛
⎝

E∧B

B²

⎞
⎠

(2.132)

In the frame of the guiding centre which is accelerating, a force is felt.

F_a = − m

⎛
⎝

E∧B

B²

⎞
⎠

(Pushed back into seat! −ve.)

(2.133)

This force produces another drift

v_D

F_a ∧B

B²

= −

qB²

⎛
⎝

E∧B

B²

⎞
⎠

∧B

(2.134)

−

qB²

⎛
⎝

⎞
⎠

−E

⎞
⎠

(2.135)

q B²

⋅

⊥

(2.136)

This is called the `polarization drift'.

v_D = v_{E ∧B}

v_p =

E∧B

B²

q B²

⋅

⊥

(2.137)

E ∧B

B²

ΩB

⋅

⊥

(2.138)

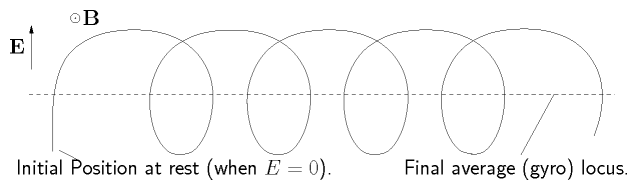
Figure 2.19: Suddenly turning on an electric field causes a shift of the gyrocenter in the direction of force. This is the polarization drift.

Start-up effect: When we `switch on' an electric field the average position (gyro center) of an initially stationary particle shifts over by ∼ ¹/₂ the orbit size. The polarization drift is this polarization effect on the medium.

Total shift due to v_p is

∆r =

⌠
⌡

v_p dt =

q B²

⌠
⌡

⊥

dt =

q B²

[ ∆E_⊥ ] .

(2.139)

2.8.1 Direct Derivation of [(dE)/dt] effect: `Polarization Drift'

Consider an oscillatory field E = Ee^−iωt (⊥r₀B)

q ( E+ v∧B)

(2.140)

q ( Ee^−iωt + v∧B)

(2.141)

Try for a solution in the form

v= v_D e^−iωt + v_L

(2.142)

where, as usual, v_L satisfies m · v_L = q v_L ∧B

Then

(1) m(−i ωv_D) = q ( E+ v_D ∧B) ×e^{−i ωt}

(2.143)

Solve for v_D: Take ∧B this equation:

(2) − m i ω( v_D ∧B) = q ( E∧B+ ( B. v_D ) B−B² v_D )

(2.144)

add m i ω×(1) to q ×(2) to eliminate v_D ∧B.

m² ω² v_D + q² ( E∧B− B² v_D ) = mi ωq E

(2.145)

or: v_D

⎡
⎣

1 −

m² ω²

q² B²

⎤
⎦

= −

miω

qB²

E+

E∧B

B²

(2.146)

i.e. v_D

⎡
⎣

1 −

ω²

Ω²

⎤
⎦

= −

iωq

ΩB |q |

E+

E∧ B

B²

(2.147)

Since −iω↔ [(∂)/(∂t)] this is the same formula as we had before: the sum of polarization and E∧B drifts except for the [1 − ω²/Ω²] term.

This term comes from the change in v_D with time (accel).

Thus our earlier expression was only approximate. A good approx if ω << Ω.

2.9 Non Uniform E (Finite Larmor Radius)

= q ( E(r) + v∧B)

(2.148)

Seek the usual solution v = v_D + v_L.

Then average out over a gyro orbit

〈m

dv_D

〉

0 = 〈q ( E(r) + v∧B) 〉

(2.149)

q [ 〈E(r) 〉+ v_D ∧B]

(2.150)

Hence drift is obviously

v_D =

〈E(r) 〉∧B

B²

(2.151)

So we just need to find the average E field experienced.

Expand E as a Taylor series about the G.C.

E(r) = E₀ +( r. ∇) E+

⎛
⎝

x²∂²

2!∂x²

y²

∂²

∂y²

⎞
⎠

E+ cross terms + .

(2.152)

(E.g. cross terms are x y [(∂²)/(∂x ∂y)]E).

Average over a gyro orbit: r = r_L (cosθ, sinθ,0).

Average of cross terms = 0.

Then

〈E(r) 〉 = E+ ( 〈r_L 〉. ∇) E+

〈r_L²〉

∇² E.

(2.153)

linear term 〈r_L〉 = 0. So

〈E(r)〉 ≅ E+

r_L²

∇² E

(2.154)

Hence E∧B with 1st finite-Larmor-radius correction is

v_{E ∧B} =

⎛
⎝

1 +

r_L²

∇²

⎞
⎠

E∧B

B²

(2.155)

[Note: Grad B drift is a finite Larmor effect already.]

Second and Third Adiabatic Invariants

There are additional approximately conserved quantities like μ in some geometries.

2.10 Summary of Drifts

v_E

E∧B

B²

Electric Field

(2.156)

v_F

F ∧B

B²

General Force

(2.157)

v_E

⎛
⎝

1 +

r_L²

∇²

⎞
⎠

E∧B

B²

Nonuniform E

(2.158)

v_∇B

mv_⊥²

B∧∇ B

B³

Grad B

(2.159)

v_R

mv_||²

R_c ∧B

R_c² B²

Curvature

(2.160)

v_R + v_∇B

⎛
⎝

mv_||² +

m v_⊥²

⎞
⎠

R_c ∧B

R_c² B²

Vacuum Fields.

(2.161)

v_p

|q |

⋅

⊥

|Ω|B

Polarization

(2.162)

Mirror Motion

μ ≡

mv_⊥²

is constant

(2.163)

Force is F = − μ∇B.

HEAD

Chapter 2 Motion of Charged Particles in Fields

2.1 Uniform B field, E = 0.

2.1.1 Qualitatively

2.1.2 By Vector Algebra

2.2 Uniform B and non-zero E

2.2.1 Drift due to Gravity or other Forces

2.3 Non-Uniform B Field

Algebra

2.4 Curvature Drift

2.4.1 Vacuum Fields

2.5 Interlude: Toroidal Confinement of Single Particles

2.5.1 How to solve this problem?

2.5.2 The Solution: Rotational Transform

Rotational Transform

`Safety Factor'

2.6 The Mirror Effect of Parallel Field Gradients: E = 0, ∇B ||B

2.6.1 Force on an Elementary Magnetic Moment Circuit

2.6.2 μ is a constant of the motion

Proof from F||

Angular Momentum

Proof direct from Angular Momentum

2.6.3 Mirror Trapping

Pitch Angle θ

2.6.4 Other Features of Mirror Motions

2.7 Time Varying B Field (E inductive)

2.8 Time Varying E-field (E, B uniform)

2.8.1 Direct Derivation of [(dE)/dt] effect: `Polarization Drift'

2.9 Non Uniform E (Finite Larmor Radius)

2.10 Summary of Drifts

Chapter 2
Motion of Charged Particles in Fields

Proof from F_||